Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng đi qua hai điểm A(1; 2) và B(3; 6)?
![]()
![]()
![]()
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có ![]() đây là 1 VTCP của đường thẳng đã cho.
đây là 1 VTCP của đường thẳng đã cho.
Suy ra đường thẳng đã cho có 1 VTPT là ![]() ( 4; -2)
( 4; -2)
Lại có vecto ![]() cùng phương với VTPt trên nên vecto
cùng phương với VTPt trên nên vecto ![]() cũng là 1 VTPT của đường thẳng đã cho.
cũng là 1 VTPT của đường thẳng đã cho.
Chọn C.

Đáp án A
Từ giả thiết ta suy ra hai đường thẳng d và d’ đồng phẳng, do đó khẳng định A là sai.


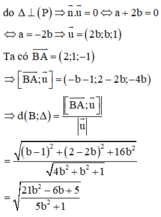

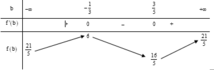
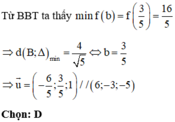
Chú ý khi giải: Các em có thể tham khảo cách 2:
+) Lập phương trình mặt phẳng (Q) đi qua A và song song với (P).
+) Khi đó Δ cần tìm là một đường thẳng nằm trong (Q) và đi qua A.


Khi phương trình đường thẳng cho dưới dạng tham số: 
Thì đường thẳng có VTCP là ![]() (a; b)
(a; b)
Do đó; phương trình đường thẳng đã cho có vecto chỉ phương là ![]() (6; 0)
(6; 0)
Lại có: vecto ![]() cùng phương với vecto
cùng phương với vecto ![]() nên vecto
nên vecto ![]() cũng là VTCP của đường thẳng đã cho.
cũng là VTCP của đường thẳng đã cho.
Chọn D.

Chọn đáp án A
Nếu u → là một vectơ chỉ phương của đường thẳng Δ thì k u → k ≠ 0 cũng là một vectơ chỉ phương.
Đường thẳng đi qua hai điểm A và B nhận vectơ A B → = - 4 ; 4 = - 4 1 ; - 1 = - 4 a → làm một vectơ chỉ phương nên vectơ a → - 1 ; - 1 là một vectơ chỉ phương.
Ta có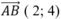 là 1 VTCP của đường thẳng đã cho.
là 1 VTCP của đường thẳng đã cho.
Chọn A.