Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = 3sin x + 4cos x + 1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

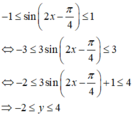
Giá trị lớn nhất và nhỏ nhất của hàm số đã cho là: 4 và - 2
Đáp án A

\(y=5\left[\dfrac{3}{5}sin\left(3x+\dfrac{\pi}{6}\right)+\dfrac{4}{5}cos\left(3x+\dfrac{\pi}{6}\right)\right]\)
\(y=5.sin\left(3x+\dfrac{\pi}{6}+a\right)\) với \(cosa=\dfrac{3}{5}\)
Do \(-1\le sin\left(3x+\dfrac{\pi}{6}+a\right)\le1\)
\(\Rightarrow-5\le y\le5\)

a: ĐKXĐ: 2x<>kpi và cot2x<>-1/căn 3
=>x<>kpi/2 và 2x<>-pi/3+kpi
=>x<>kpi/2 và x<>-pi/6+kpi/2
b: -1<=cos(2x+pi/5)<=1
=>-4<=4cos(2x+pi/5)<=4
=>5<=y<=13
y=5 khi 2x+pi/5=pi+k2pi
=>x=2/5pi+kpi
y=13 khi 2x+pi/5=k2pi
=>x=kpi-pi/10

Câu 1:
$y=-2x^2+4x+3=5-2(x^2-2x+1)=5-2(x-1)^2$
Vì $(x-1)^2\geq 0$ với mọi $x\in\mathbb{R}$ nên $y=5-2(x-1)^2\leq 5$
Vậy $y_{\max}=5$ khi $x=1$
Hàm số không có min.
Câu 2:
Hàm số $y$ có $a=-3<0; b=2, c=1$ nên đths có trục đối xứng $x=\frac{-b}{2a}=\frac{1}{3}$
Lập BTT ta thấy hàm số đồng biến trên $(-\infty; \frac{1}{3})$ và nghịch biến trên $(\frac{1}{3}; +\infty)$
Với $x\in (1;3)$ thì hàm luôn nghịch biến
$\Rightarrow f(3)< y< f(1)$ với mọi $x\in (1;3)$
$\Rightarrow$ hàm không có min, max.

\(-1\le sin\left(x^2\right)\le1\Rightarrow\)\(0\le\sqrt{1-sin\left(x^2\right)}\le\sqrt{2}\Rightarrow-1\le y\le\sqrt{2}-1\)
\(y_{min}=-1\) khi \(sin\left(x^2\right)=1\Rightarrow x=\pm\sqrt{\dfrac{\pi}{2}+k2\pi}\) (\(k\in N\))
\(y_{max}=\sqrt{2}-1\) khi \(sin\left(x^2\right)=-1\Rightarrow x=\pm\sqrt{-\dfrac{\pi}{2}+k2\pi}\) (\(k\in Z^+\))


Đáp án C