Để phương trình z 2 + b z + c = 0 nhận z 1 = - 4 + 2 i và z 2 = - 4 - 2 i làm nghiệm thì
A. b = -8, c = 20
B. b = -8, c = -20
C. b = 8, c = 20
D. b = 8, c = 20
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


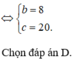

Nếu \(z_1=a+bi\) là nghiệm thì \(z_2=a-bi\) cũng là nghiệm, do đó \(1-i\) cũng là nghiệm
\(\Rightarrow\left\{{}\begin{matrix}-a=z_1+z_2=2\\b=z_1z_2=2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=-2\\b=2\end{matrix}\right.\)
\(\Rightarrow a-b=-4\)

Chọn A
Ta có z = 1 - 2i là nghiệm của phương trình đã cho nên:
( 1 - 2 i ) 2 + a ( 1 - 2 i ) + b = 0 <=> (a + b - 3) - (2a + 4)i = 0
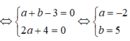
Vậy: a + b = -2 + 5 = 3

Đáp án C
A. z=a+bi hoặc z=-a-bi (loại)
B. ![]() (loại)
(loại)
C. giải phương trình bậc hai ẩn z có nghiệm z=a+bi; z=a-bi (thỏa mãn)

Ta có:\(x^2+4y+4=0;y^2+4z+4=0;z^2+4x+4=0\)
\(\Leftrightarrow\left(x^2+4y+4\right)+\left(y^2+4z+4\right)+\left(z^2+4x+4\right)=0\)
\(\Leftrightarrow x^2+4x+4+y^2+4y+4+z^2+4z+4=0\)
\(\Leftrightarrow\left(x+2\right)^2+\left(y+2\right)^2+\left(z+2\right)^2=0\)
Mà\(\left(x+2\right)^2\ge0;\left(y+2\right)^2\ge0;\left(z+2\right)^2\ge0\)
\(\Leftrightarrow\left(x+2\right)^2+\left(y+2\right)^2+\left(z+2\right)^2\ge0\)
Dấu "=" xảy ra\(\Leftrightarrow\hept{\begin{cases}x+2=0\\y+2=0\\z+2=0\end{cases}\Leftrightarrow\hept{\begin{cases}x=-2\\y=-2\\z=-2\end{cases}\Leftrightarrow}x=y=z=-2}\)
Vậy\(x^{10}+y^{10}+z^{10}=x^{10}+x^{10}+x^{10}\)
\(=3\cdot x^{10}=3\cdot\left(-2\right)^{10}=3\cdot1024=3072\)