Hãy nhắc lại:
a) Các hằng đẳng thức lượng giác cơ bản;
b) Công thức cộng;
c) Công thức nhân đôi;
d) Công thức biến đổi tích thành tổng và tổng thành tích.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



cosα = OH¯; sinα = OK¯
Do tam giác OMK vuông tại K nên:
sin2 α + cos2 α = OK¯2 + OH¯2 = OK2 + MK2 = OM2 = 1.
Vậy sin2 α + cos2 α = 1.
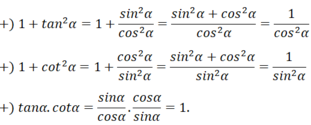

Ta có: x - x 2 = x 1 - x
(Tử thức của phân thức bên phải bằng tử thức của phân thức bên trái chia cho (1 – x).
Do đó ta chia cả tử và mẫu của phân thức bên trái cho 1 – x thì thu được phân thức bên phải.)
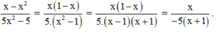
Vậy đa thức cần điền là -5x – 5.

3 x 3 + 24 x = 3 x . x 2 + 8
(Tử thức của phân thức bên phải bằng tử thức của phân thức bên trái nhân với 3x.
Do đó ta nhân cả tử và mẫu của phân thức bên trái với 3x thì thu được phân thức bên phải)
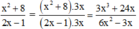
Vậy đa thức cần điền là 6 x 2 - 3 x

3 y - x 2 = 3 . x - y 2 = x - y . 3 x - y
(Mẫu thức của phân thức bên trái bằng mẫu thức của phân thức bên phải chia cho 3(x – y)
Do đó ta chia cả tử và mẫu của phân thức bên phải cho 3(x – y) để thu được phân thức bên trái)
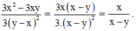
Vậy đa thức cần điền là x.

y 2 - x 2 = y - x y + x
(Mẫu thức của phân thức bên phải bằng mẫu thức của phân thức bên trái nhân với (y – x).
Do đó ta nhân cả tử và mẫu của phân thức bên trái với (y – x) để thu được phân thức bên phải)
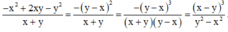
Vậy đa thức cần điền là x - y 3

- Nếu ta nhân cả tử và mẫu của một phân số với cùng một số nguyên khác 0 thì ta được một phân số bằng phân số đã cho.
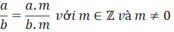
- Nếu ta chia cả tử và mẫu của một phân số cho cùng một ước chung của chúng thì ta được một phân số bằng phân số đã cho.


`1)(a^[1/4]-b^[1/4])(a^[1/4]+b^[1/4])(a^[1/2]+b^[1/2])`
`=[(a^[1/4])^2-(b^[1/4])^2](a^[1/2]+b^[1/2])`
`=(a^[1/2]-b^[1/2])(a^[1/2]+b^[1/2])`
`=a-b`
`2)(a^[1/3]-b^[2/3])(a^[2/3]+a^[1/3]b^[2/3]+b^[4/3])`
`=(a^[1/3]-b^[2/3])[(a^[1/3])^2+a^[1/3]b^[2/3]+(b^[2/3])^2]`
`=(a^[1/3])^3-(b^[2/3])^3`
`=a-b^2`
a) Các hằng đẳng thức lượng giác cơ bản:
sin2α + cos2α = 1
1 + tan2α = 1/(cos2α); α ≠ π/2 + kπ, k ∈ Z
1 + cot2α = 1/(sin2α); α ≠ kπ, k ∈ Z
tanα.cotα = 1; α ≠ kπ/2, k ∈ Z
b) Công thức cộng:
cos(a - b) = cosa cosb + sina sinb
cos(a + b) = cosa cosb - sina sinb
sin(a - b) = sina cosb - cosa sinb
sin(a + b) = sina.cosb + cosa.sinb
c) Công thức nhân đôi:
sin2α = 2 sinα cosα
cos2α = cos2α - sin2α = 2cos2α - 1 = 1 - 2sin2α
d) Công thức biến đổi tích thành tổng:
cos a cosb = 1/2 [cos(a - b) + cos(a + b) ]
sina sinb = 1/2 [cos(a - b) - cos(a + b) ]
sina cosb = 1/2 [sin(a - b) + sin(a + b) ]
Công thức biến đổi tổng thành tích: