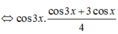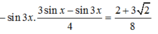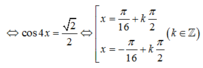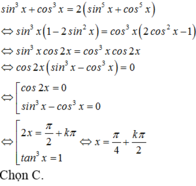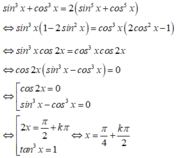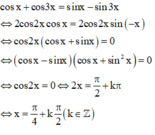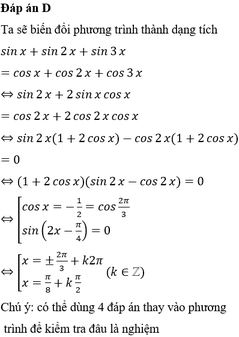Giải phương trình √3 sin3x – cos3x = √2.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
22 tháng 10 2018
Đúng(0)
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 8 2021
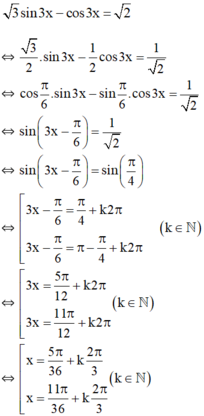
ĐKXĐ: ...
\(sin3x-cos3x+sinx+cosx=\dfrac{sin3x-cos3x+sinx+cosx}{\left(sin3x+cosx\right)\left(cos3x-sinx\right)}\)
\(\Rightarrow\left[{}\begin{matrix}sin3x-cos3x+sinx+cosx=0\left(1\right)\\\left(sin3x+cosx\right)\left(cos3x-sinx\right)=1\left(2\right)\end{matrix}\right.\)
(1) \(\Leftrightarrow3sinx-4sin^3x-4cos^3x+3cosx+sinx+cosx=0\)
\(\Leftrightarrow sinx+cosx+sin^3x+cos^3x=0\)
\(\Leftrightarrow sinx+cosx+\left(sinx+cosx\right)\left(1-sinx.cosx\right)=0\)
\(\Leftrightarrow\left(sinx+cosx\right)\left(2-sinx.cosx\right)=0\)
\(\Leftrightarrow sinx+cosx=0\) (loại)
(2) \(\Leftrightarrow sin3x.cos3x-sinx.cosx-sin3x.sinx+cos3x.cosx=1\)
\(\Leftrightarrow\dfrac{1}{2}sin6x-\dfrac{1}{2}sin2x+cos4x=1\)
\(\Leftrightarrow\dfrac{1}{2}\left(3sin2x-4sin^32x\right)-\dfrac{1}{2}sin2x+1-2sin^22x=1\)
\(\Leftrightarrow sin2x-2sin^32x-2sin^22x=0\)
\(\Leftrightarrow-sin2x\left(2sin^22x+2sin2x-1\right)=0\)
\(\Leftrightarrow...\)
HY
1
13 tháng 12 2022
\(\Rightarrow\sqrt{2}.sin\left(3x-\dfrac{\pi}{4}\right)-\sqrt{2}.sin\left(5x-\dfrac{\pi}{3}\right)=0\Leftrightarrow sin\left(3x-\dfrac{\pi}{4}\right)=sin\left(5x-\dfrac{\pi}{3}\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-\dfrac{\pi}{4}+k2\pi=5x-\dfrac{\pi}{3}\\\pi-3x+\dfrac{\pi}{4}+k2\pi=5x-\dfrac{\pi}{3}\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=\dfrac{\pi}{12}+k\pi\\x=\dfrac{19\pi}{96}+\dfrac{k\pi}{4}\end{matrix}\right.\); k\(\in Z\)
HA
1
1 tháng 9 2023
\(PT\Leftrightarrow\left\{{}\begin{matrix}sin3x+cos3x>=0\\2\cdot\left(sin3x+cos3x\right)^2=1+2\cdot sin6x+2\cdot sin2x\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}sin3x+cos3x>=0\\2+2\cdot sin6x=1+2\cdot sin6x+2\cdot sin2x\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}sin3x+cos3x>=0\left(1\right)\\sin2x=\dfrac{1}{2}\left(2\right)\end{matrix}\right.\)
(2): sin2x=1/2
=>2x=pi/6+k2pi hoặc 2x=5/6pi+k2pi
=>x=pi/12+kpi hoặc x=5/12pi+kpi
Khi x=pi/12+kpi thì:
\(sin3x+cos3x=sin\left(\dfrac{pi}{4}+3\cdot kpi\right)+cos\left(\dfrac{pi}{4}+3\cdot kpi\right)\)
Để sin 3x+cos3x>=0 thì k=2n
Khi x=5/12pi+kpi thì \(sin3x+cos3x=sin\left(\dfrac{5}{4}pi+3\cdot kpi\right)+cos\left(\dfrac{5}{4}pi+3\cdot k\cdot pi\right)\)
Để sin 3x+cos3x>=0 thì \(k=2n+1\)
=>Phương trình ban đầu sẽ có các nghiệm là: \(x=\dfrac{pi}{12}+2npi;x=\dfrac{17}{12}pi+2npi\)
PT
1
CM
26 tháng 2 2018
Chọn D
Ta sẽ biến đổi phương trình thành dạng tích
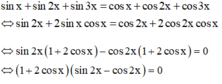
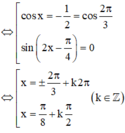
Chú ý: có thể dùng 4 đáp án thay vào phương trình để kiểm tra đâu là nghiệm
