Cho hình 70 trong đó hai đường tròn cùng có tâm là O. Cho biết AB > CD.
Hãy so sánh các độ dài:
ME và MF
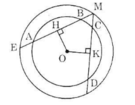
Hình 70
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
28 tháng 11 2019
a) Trong đường tròn nhỏ:
AB > CD => OH < OK (định lí 3)
b) Trong đường tròn lớn:
OH < OK => ME > MF (định lí 3)
c) Trong đường tròn lớn:
ME > MF => MH > MK
30 tháng 4 2021
a) Trong đường tròn nhỏ:
AB > CD => OH < OK (định lí 3)
b) Trong đường tròn lớn:
OH < OK => ME > MF (định lí 3)
c) Trong đường tròn lớn:
ME > MF => MH > MK
DH
30 tháng 4 2021
a) Xét trong đường tròn nhỏ:
Theo định lí : trong hai dây của một đường tròn, dây nào lớn hơn thì dây đó gần tâm hơn.
Theo giả thiết suy ra gần tâm hơn, tức là .
b) Xét trong đường tròn lớn:
Theo định lí : trong hai dây của một đường tròn, dây nào gần tâm hơn thì dây đó lớn hơn.
Theo câu , ta có: .
c) Xét trong đường tròn lớn:
Vì (Định lý 2 - trang 103).
Vì (Định lý 2 - trang 103).
Theo câu , ta có:
KD
25 tháng 4 2017
a) Xét đường tròn nhỏ ta được .
b) Xét đường tròn lớn ta được .
c) Từ kết quả câu b) suy ra .
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 7 2021
Từ O kẻ đường thẳng vuông góc AB và CD, cắt AB và CD lần lượt tại H và K
\(\Rightarrow\) H là trung điểm AB và K là trung điểm CD
\(\Rightarrow\left\{{}\begin{matrix}AH=\dfrac{1}{2}AB=4\\CK=\dfrac{1}{2}CD=4,8\end{matrix}\right.\)
Áp dụng định lý Pitago cho tam giác vuông OAH (với chú ý \(OA=OC=R=5\))
\(OH=\sqrt{OA^2-AH^2}=3\left(cm\right)\)
Pitago tam giác OCK:
\(OK=\sqrt{OC^2-CK^2}=1,4\left(cm\right)\)
\(\Rightarrow HK=OH+OK=4,4\left(cm\right)\)
Trong đường tròn lớn:
OH < OK => ME > MF (định lí 3)