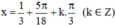Giải phương trình sau: c o t 3 x - 1 = - 3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
24 tháng 2 2021
`a,(x+3)(x^2+2021)=0`
`x^2+2021>=2021>0`
`=>x+3=0`
`=>x=-3`
`2,x(x-3)+3(x-3)=0`
`=>(x-3)(x+3)=0`
`=>x=+-3`
`b,x^2-9+(x+3)(3-2x)=0`
`=>(x-3)(x+3)+(x+3)(3-2x)=0`
`=>(x+3)(-x)=0`
`=>` $\left[ \begin{array}{l}x=0\\x=-3\end{array} \right.$
`d,3x^2+3x=0`
`=>3x(x+1)=0`
`=>` $\left[ \begin{array}{l}x=0\\x=-1\end{array} \right.$
`e,x^2-4x+4=4`
`=>x^2-4x=0`
`=>x(x-4)=0`
`=>` $\left[ \begin{array}{l}x=0\\x=4\end{array} \right.$
24 tháng 2 2021
1) a) \(\left(x+3\right).\left(x^2+2021\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x+3=0\\x^2+2021=0\end{matrix}\right.\\\left[{}\begin{matrix}x=-3\left(nhận\right)\\x^2=-2021\left(loại\right)\end{matrix}\right. \)
=> S={-3}
16 tháng 8 2021
a: Ta có: \(8x+11-3=5x+x-3\)
\(\Leftrightarrow8x+8=6x-3\)
\(\Leftrightarrow2x=-11\)
hay \(x=-\dfrac{11}{2}\)
b: Ta có: \(2x\left(x+2\right)^2-8x^2=2\left(x-2\right)\left(x^2+2x+4\right)\)
\(\Leftrightarrow2x\left(x^3+6x^2+12x+8\right)-8x^2=2\left(x^3-8\right)\)
\(\Leftrightarrow2x^4+12x^3+24x^2+16x-8x^2-2x^3+16=0\)
\(\Leftrightarrow2x^4+10x^3+16x^2+16x+16=0\)
\(\Leftrightarrow2x^4+4x^3+6x^3+12x^2+4x^2+8x+8x+16=0\)
\(\Leftrightarrow\left(x+2\right)\left(2x^3+6x^2+4x+8\right)=0\)
\(\Leftrightarrow x+2=0\)
hay x=-2
16 tháng 8 2021
c: Ta có: \(\left(x+1\right)\left(2x-3\right)=\left(2x-1\right)\left(x+5\right)\)
\(\Leftrightarrow2x^2-3x+2x-3-2x^2-10x+x+5=0\)
\(\Leftrightarrow-10x+2=0\)
\(\Leftrightarrow-10x=-2\)
hay \(x=\dfrac{1}{5}\)
d: Ta có: \(\dfrac{1}{10}-2\cdot\left(\dfrac{1}{2}t-\dfrac{1}{10}\right)=2\left(t-\dfrac{5}{2}\right)-\dfrac{7}{10}\)
\(\Leftrightarrow\dfrac{1}{10}-t+\dfrac{1}{5}=2t-5-\dfrac{7}{10}\)
\(\Leftrightarrow-t-2t=-\dfrac{57}{10}-\dfrac{3}{10}=-6\)
hay t=2
Y
12 tháng 4 2022
\(a,\dfrac{x-3}{x}=\dfrac{x-3}{x+3}\)\(\left(đk:x\ne0,-3\right)\)
\(\Leftrightarrow\dfrac{x-3}{x}-\dfrac{x-3}{x+3}=0\)
\(\Leftrightarrow\dfrac{\left(x-3\right)\left(x+3\right)-x\left(x-3\right)}{x\left(x+3\right)}=0\)
\(\Leftrightarrow x^2-9-x^2+3x=0\)
\(\Leftrightarrow3x-9=0\)
\(\Leftrightarrow3x=9\)
\(\Leftrightarrow x=3\left(n\right)\)
Vậy \(S=\left\{3\right\}\)
Y
12 tháng 4 2022
\(b,\dfrac{4x-3}{4}>\dfrac{3x-5}{3}-\dfrac{2x-7}{12}\)
\(\Leftrightarrow\dfrac{4x-3}{4}-\dfrac{3x-5}{3}+\dfrac{2x-7}{12}>0\)
\(\Leftrightarrow\dfrac{3\left(4x-3\right)-4\left(3x-5\right)+2x-7}{12}>0\)
\(\Leftrightarrow12x-9-12x+20+2x-7>0\)
\(\Leftrightarrow2x+4>0\)
\(\Leftrightarrow2x>-4\)
\(\Leftrightarrow x>-2\)
S
23 tháng 2 2021
Mình khuyên bạn thế này :
Bạn nên tách những câu hỏi ra
Như vậy các bạn sẽ dễ giúp
Và cũng có nhiều bạn giúp hơn !
23 tháng 2 2021
Bài 1.
a) ( x - 3 )( x + 7 ) = 0
<=> x - 3 = 0 hoặc x + 7 = 0
<=> x = 3 hoặc x = -7
Vậy S = { 3 ; -7 }
b) ( x - 2 )2 + ( x - 2 )( x - 3 ) = 0
<=> ( x - 2 )( x - 2 + x - 3 ) = 0
<=> ( x - 2 )( 2x - 5 ) = 0
<=> x - 2 = 0 hoặc 2x - 5 = 0
<=> x = 2 hoặc x = 5/2
Vậy S = { 2 ; 5/2 }
c) x2 - 5x + 6 = 0
<=> x2 - 2x - 3x + 6 = 0
<=> x( x - 2 ) - 3( x - 2 ) = 0
<=> ( x - 2 )( x - 3 ) = 0
<=> x - 2 = 0 hoặc x - 3 = 0
<=> x = 2 hoặc x = 3
QT
Quoc Tran Anh Le
Giáo viên
21 tháng 9 2023
a) Với mọi \(x \in \mathbb{R}\) ta có \( - 1 \le cosx \le 1\)
Vậy phương trình \(cosx = - 3\;\) vô nghiệm.
\(\begin{array}{l}b)\,\;cosx = cos{15^o}\;\\ \Leftrightarrow \left[ \begin{array}{l}x = {15^o} + k{360^o},k \in \mathbb{Z}\\x = - {15^o} + k{360^o},k \in \mathbb{Z}\end{array} \right.\end{array}\)
Vậy phương trình có nghiệm \(x = {15^o} + k{360^o}\) hoặc \(x = - {15^o} + k{360^o},k \in \mathbb{Z}\).
\(\begin{array}{l}c)\;\,cos(x + \frac{\pi }{{12}}) = cos\frac{{3\pi }}{{12}}\\ \Leftrightarrow \left[ \begin{array}{l}x + \frac{\pi }{{12}} = \frac{{3\pi }}{{12}} + k2\pi ,k \in \mathbb{Z}\\x + \frac{\pi }{{12}} = - \frac{{3\pi }}{{12}} + k2\pi ,k \in \mathbb{Z}\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{6} + k2\pi ,k \in \mathbb{Z}\\x = - \frac{\pi }{3} + k2\pi ,k \in \mathbb{Z}\end{array} \right.\end{array}\)
Vậy phương trình có nghiệm \(x = \frac{\pi }{6} + k2\pi ,\) hoặc \(x = - \frac{\pi }{3} + k2\pi ,k \in \mathbb{Z}\).
8 tháng 3 2023
a: =>3x=-25
=>x=-25/3
b: =>(x-5)(4x+3-31)=0
=>(4x-28)(x-5)=0
=>x=5 hoặc x=7
c: =>3x-3-x-3=5x-33
=>2x-6=5x-33
=>-3x=-27
=>x=9(nhận)
DT
0
N
giải các Phương trình sau
a) (5x+3)(x2+1)(x-1)=0
b) (4x-1)(x-3)-(x-3)(5x+2)=0
c) (x+6)(3x-1)+x2-36 =0
1
23 tháng 2 2023
a: =>(5x+3)(x-1)=0
=>x=1 hoặc x=-3/5
b: =>(x-3)(4x-1-5x-2)=0
=>(x-3)(-x-3)=0
=>x=-3 hoặc x=3
c: =>(x+6)(3x-1+x-6)=0
=>(x+6)(4x-7)=0
=>x=7/4 hoặc x=-6
Điều kiện: 3x - 1 ≠ kπ ∀ k ∈ Z
Mọi giá trị thuộc họ nghiệm đều thỏa mãn điều kiện xác định.
Vậy phương trình có họ nghiệm