Công thức tính tổng của dãy là gì đấy mọi người đúng vào nhé
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
27 tháng 4 2018
*. TỔNG = (Số đầu + số cuối) x Số số hạng : 2
*. SỐ CUỐI = Số đầu + Đơn vị khoảng cách x (số số hạng - 1)
*. SỐ ĐẦU = Số cuối - Đơn vị khoảng cách x (số số hạng - 1)
*. SỐ SỐ HẠNG = (Số cuối – Số đầu) : Đơn vị khoảng cách + 1
*. TRUNG BÌNH CỘNG = Trung bình cộng của số đầu và số cuối.
30 tháng 12 2016
Muốn tính tổng của một dãy số có quy luật cách đều chúng ta thường tính theo các bước như sau: Bước 1: Tính số số hạng có trong dãy: (Số hạng lớn nhất của dãy - số hạng bé nhất của dãy) : khoảng cách giữa hai số hạng liên tiếp trong dãy + 1 Bước 2: Tính tổng của dãy: (Số hạng lớn nhất của dãy + số hạng bé nhất của dãy) x số số hạng có trong dãy : 2 |
k mk nha
DB
30 tháng 12 2016
tổng là số đầu cộng số cuối nhân số số hạng chia đôi
k mk nhe
CM
5 tháng 1 2020
Chọn B
Ta có 2n+1 – (n+1)2n= 4(2n – n.2n-1 )- 4(2n-1 – (n-1)2n-2) → un= 2n – n.2n-1
30 tháng 3 2021
Mình nghĩ mình sẽ không đưa code, mà chỉ đưa ý tưởng thôi nhé.
1. Khai báo n, mảng a và s = 0. Với mỗi phần tử a, ta cộng nó vào s. Cuối ta in ra s/n.
2. Cũng khai báo n, mảng a và 2 biến s1 (lưu tổng lẻ) và s2 (lưu tổng chẵn). Với mỗi a, ta kiểm tra số đó có phải là số chẵn hay lẻ (if n mod 2 = 0) và cộng vào s1 (nếu là chẵn) hoặc s2 (nếu là lẻ) và in ra.
3. Khai báo n, mảng a và minn để chứa số nhỏ nhất. Với mỗi a, tìm minn bằng cách so sánh a với minn và gán lại minn nếu nó lớn hơn a. Sau đó cho chạy thêm một vòng nữa để kiểm tra xem số nào là số minn, và in chỉ số của nó ra.
Nếu có gì thắc mắc, hỏi kỹ mình, mình sẽ giúp đỡ nhé.
Chúc bạn học tốt 
.
30 tháng 3 2021
Câu 1:
uses crt;
var n,i,t:integer;
a:array[1..100]of integer;
begin
clrscr;
write('Nhap n='); readln(n);
for i:=1 to n do
begin
write('A[',i,']='); readln(a[i]);
end;
t:=0;
for i:=1 to n do
t:=t+a[i];
writeln(t/n:4:2);
readln;
end.
CM
26 tháng 12 2018
Chọn B
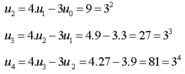
Dự đoán ta được u n = 3 n
Lại có 3 n + 1 = 4.3 n − 3.3 n − 1
Vậy u n = 3 n
NQ
1
H
19 tháng 1 2021
Đây bạn:
Xác định số ảnh, vị trí ảnh của một vật qua gương phẳng?
Phương pháp giải: Dựa vào tính chất ảnh của một vật qua gương phẳng: “ảnh của một vật qua gương phẳng bằng vật và cách vật một khoảng bằng từ vật đến gương” (ảnh và vật đối xứng nhau qua gương phẳng)
Ví dụ 1: Hai gương phẳng M và N đặt hợp với nhau một góc a < 180độ, mặt phản xạ quay vào nhau. Một điểm sáng A nằm giữa hai gương và qua hệ hai gương cho n ảnh. Chứng minh rằng nếu 360/a=2k(k thuộc N) thì n = (2k – 1) ảnh.
Giải Sơ đồ tạo ảnh qua hệ:
A---------->A1-------->A3---------->A5----------->...
A---------->A2-------->A4---------->A6----------->...
Từ bài toán ta có thể biễu diễn một số trường hợp đơn giản. Theo hình vẽ ta có:(Hình vẽ ở phía dưới).
Góc A1OA2 = 2a
Góc A3OA4 = 4a
......
Góc A2k-1OA2k = 2ka
Theo điều kiện bài toán thì 360 độ/a = 2k
=> 2ka = 360độ. Vậy góc A2k-1OA2k = 2k = 360độ
Tức là ảnh A2k-1 và ảnh A2k trùng nhau 
12 tháng 11 2015
tính số lượng số hạng dãy số cách đều = ( số đầu - số cuối ) : khoảng cách +1
tính tổng = số số hạng x TBC của số đầu và số cuối
cộng tất cả các số trong dãy lại là ra