Một chiếc ô tô đang chạy với vận tốc 16m/s và gia tốc 2 m / s 2 thì tăng tốc cho đến khi đạt được vận tốc 24m/s thì bắt đầu giảm tốc độ cho đến khi dừng hẳn. Biết ô tô bắt đầu tăng vận tốc cho đến khi dừng hẳn là 10s. Hỏi quãng đường của ô tô đã chạy.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
8 tháng 4 2018
Chọn đáp án C
Lời giải:
+ Áp dụng công thức v = v 0 + a t 1 ⇒ 24 = 16 + 2 . t 1 ⇒ t 1 = 4 s là thời gian tăng tốc độ.
Vậy thời gian giảm tốc độ: t 2 = t – t 1 = 6 s
Quãng đường đi được khi ô tô tăng tốc độ: S 1 = v 0 t 1 + 1 2 a t 1 2 ⇒ S 1 = 16.4 + 1 2 .2.4 2 = 80 m
Quãng đường đi được từ khi bắt đầu giảm tốc độ đến khi dừng hẳn:
S 2 = v 1 t 2 + 1 2 a t 2 2 ⇒ S 2 = 24.6 − 1 2 .2.6 2 = 108 m
⇒ S = S 1 + S 2 = 80 + 108 = 188 m
Chọn đáp án C
N
17 tháng 6 2018
Tóm tắt:
v1 = 16m/s
a1 = 2m/s2
v2 = 24m/s
v3 = 0m/s
a2 = ? m/s2
s1 = ? m
s2 = ? m
t1 + t2 = t = 10 giây
-----------------------------------------
Lúc đầu: Ta có quãng đường chiếc ca-nô chuyển động nhanh dần đều là:
v22 - v12 = 2a1.s1 ⇒ s1 = \(\dfrac{v_2^2-v_1^2}{2a_1}\) = \(\dfrac{24^2-16^2}{2.2}\) = 80(m)
Ta lại có: s1 = v1.t1 + \(\dfrac{1}{2}\)a1.t12 ⇔ 80 = 16.t1 + \(\dfrac{1}{2}\).2.t12
⇒ (16 + t1).t1 = 80 ⇒ t1 = 4(giây)
Mà ta có: t1 + t2 = 10 giây ⇒ t2 = 10 - 4 = 6(giây)
Lúc sau: Ca-nô chuyển động chậm đều:
Ta có: a2 = \(\dfrac{v_3-v_2}{t_2}\) = \(\dfrac{0-24}{6}\) = -4(m/s2)
Quãng đường ca-nô chuyển động chậm đều là:
s2 = v2.t1 + \(\dfrac{1}{2}\).a2.t22 = 24.4 + \(\dfrac{1}{2}\).(-4).62 = 24(m)
Vậy quãng đường ca-nô trên đã chạy là:
s = s1 + s2 = 80 + 24 = 104(m)
HH
17 tháng 6 2018
Gọi S1 là quãng đường ca nô chạy với v=16 m/s đến khi đạt được v=24m/s , S2 là quãng đường khi v=24m/s cho đến khi dừng hẳn.
- S1: ta có t1= (v-v0)/ a1= (24-16)/2= 4s
Mà tổng t = 10s => t2= 10-t1= 6s
-S2: ta có a2= (v2-v)/t2= (0-24)/6= -4 m/s (v2=0 vì cuối cùng cano dừng lại)
Ta có công thức: S=vo.t + 1/2 a.t^2
=> Quãng đường ca nô chạy = S1+S2 thế số vào.
18 tháng 12 2021
Gia tốc vật: \(v=v_0+at\)
\(\Rightarrow a=\dfrac{v-v_0}{t}=\dfrac{15-5}{20}=0,5\)m/s2
Quãng đường xe sau 20s tăng ga:
\(S=v_0t+\dfrac{1}{2}at^2=5\cdot20+\dfrac{1}{2}\cdot0,5\cdot20^2=200m\)
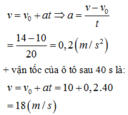
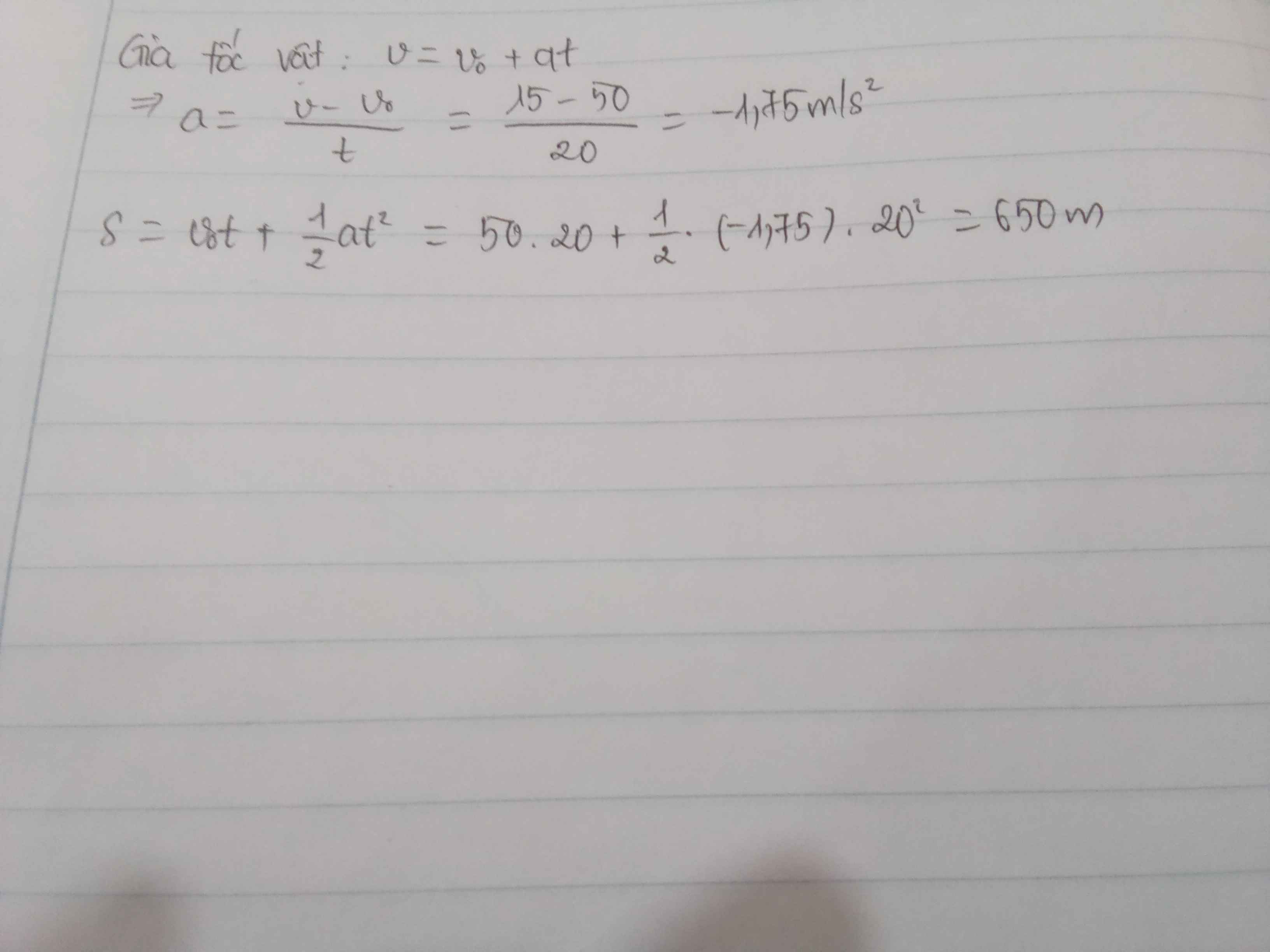
Giải: Áp dụng công thức
v = v 0 + a t 1 ⇔ 24 = 16 + 2 . t 1 ⇔ t 1 = 4 s là thời gian tăng tốc độ.
Vậy thời gian giảm tốc độ: t 2 = t – t 1 = 6 s
Quãng đường đi được khi ô tô tăng tốc độ: S 1 = v 0 t 1 + 1 2 a t 1 2 ⇒ S 1 = 16.4 + 1 2 .2.4 2 = 80 m
Quãng đường đi được từ khi bắt đầu giảm tốc độ đến khi dừng hẳn S 2 = v 1 t 2 + 1 2 a t 2 2 ⇒ S 2 = 24.6 − 1 2 .2.6 2 = 108 m
⇒ S = S 1 + S 2 = 80 + 108 = 188 m