Cho x O y ^ = 90 ° . Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B. Kẻ đường trung trực HM của đoạn thẳng OA (H thuộc OA, M thuộc AB). Chứng minh M thuộc đường trung trực của OB.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

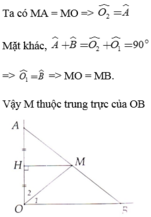

a: Xét ΔOAH và ΔOBH có
OA=OB
HA=HB
OH chung
Do đó: ΔOHA=ΔOHB

1: OM<OB
nên M nằm giữa O và B
Suy ra: MO+MB=OB
hay MB=3cm
2: MA=2+1=3cm=MB
nên M là trung điểm của AB

độ dài đoạn thẳng AB là :
AB = OA + OB = 4cm + 2cm = 6cm
độ dài đoạn thẳng NA là :
N là trung điểm của AB nên
NA = NB = \(\dfrac{AB}{2}=\dfrac{6cm}{2}=3cm\)
độ dài đoạn thẳng MA là :
M là trung điểm của AO nên
\(MA=MO=\dfrac{AO}{2}=\dfrac{4cm}{2}=2cm\)
ta có : NA = 3cm và MA = 2cm
⇒ MN = 3cm - 2cm = 1cm
Vậy MN = 1cm

a: Trên tia Oy, ta có: OB<OC
nên điểm B nằm giữa hai điểm O và C
=>OB+BC=OC
hay BC=4(cm)
Vì OA và OC là hai tia đối nhau
nên điểm O nằm giữa hai điểm A và C
=>AO+CO=AC
hay AC=8(cm)
b: Trên tia Cx, ta có: CB<CA
nên điểm B nằm giữa hai điểm C và A
mà CB=1/2CA
nên điểm B nằm giữa hai điểm C và A
c: Vì M là trung điểm của BC
nên BM=CM=BC/2=2(cm)

a, Ta có : OA + AB = OB => AB = OB - OA = 5 - 3 = 2 cm
b, Ta có : OC + OA = AC => OC = AC - OA = 6 - 3 = 3 cm
Vậy OA = OC ( 3cm = 3cm )