Một bình chứa 4,8 lít khí hiđrô ở 5 . 10 5 P a ở 14 o C . Người ta tăng nhiệt độ của khí lên tới 26 o C . Vì bình không thậ...

HD

Hoàng Đức Long

27 tháng 5 2018

Một bình chứa 4,8 lít khí hiđrô ở 5 . 10 5 P a ở 14 o C . Người ta tăng nhiệt độ của khí lên tới 26 o C . Vì bình không thật kín nên có một phần khí thoát ra ngoài và áp suất trong bình không thay đổi. Tính khối lượng khí thoát ra ngoài biết khối lượng mol của hiđrô là 2 . 10 - 3 k g / m o l ...

Đọc tiếp

#Vật lý lớp 10

1

VT

Vũ Thành Nam

27 tháng 5 2018

Đúng(0)

HD

Hoàng Đức Long

2 tháng 1 2017

Một bình chứa 4,8 lít khí hiđrô ở 5 . 10 5 P a ở 14 ∘ C . Người ta tăng nhiệt độ của khí lên tới 26 ° C . Vì bình không thật kín nên có một phần khí thoát ra ngoài và áp suất trong bình không thay đổi. Biết khối lượng mol của hiđrô là μ = 2 . 10 - 3 k g / m o l . Khối lượng khí thoát ra...

Đọc tiếp

#Vật lý lớp 10

1

VT

Vũ Thành Nam

2 tháng 1 2017

Chọn D.

Áp dụng phương trình Cla-pê-rôn – Men-đê-lê-ép:

+ Trạng thái 1 (khi chưa tăng nhiệt độ):

Khối lượng m₁, p₁ = 5.10⁵Pa, V₁ = 4,8 lít, T₁ = 287 K

Từ phương trình:

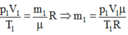
+ Trạng thái 2 (khi đã tăng nhiệt độ):

Khối lượng m₂, p₂ = p₁ = 5.10⁵Pa, V₂ = V₁ = 4,8 lít, T₂ = 26 + 273 = 287 K.

Từ phương trình:

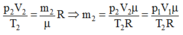
Khối lượng khí thoát ra ngoài:

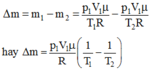
Thay số:

Đúng(0)

HD

Hoàng Đức Long

8 tháng 11 2018

Một bình chứa 14 g khí nitơ ở nhiệt độ 27 ° C và áp suất 1 atm. Sau khi hơ nóng, áp suất trong bình chứa khí tăng lên tới 5 at. Hãy tính nhiệt lượng cần cung cấp cho khí nitơ và độ tăng nội năng của khíBiết nhiệt dung riêng của nitơ trong quá trình nung nóng đẳng nhiệt là c V = 742 J/(kg.K). Coi sự nở vì nhiệt của bình là không đáng...

Đọc tiếp

#Vật lý lớp 10

1

VT

Vũ Thành Nam

8 tháng 11 2018

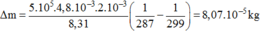
Do bình không dãn nở vì nhiệt, nên công do khí sinh ra : A' = p ∆ V = 0. Theo nguyên lí I, ta có :

∆ U = Q (1)

Nhiệt lượng do khí nhận được : Q = m c V ( T 2 - T 1 ) (2)

Mặt khác, do quá trình là đẳng tích nên :

Từ (2) tính được : Q = 15,58. 10 3 J.

Từ (1) suy ra: ∆ U = 15,58. 10 3 J.

Đúng(0)

TT

Tần Thủy Hoàng

24 tháng 2 2022

Một bình có dung tích 20 lít chứa khí ở 16⁰C dưới áp suất p. Người ta tăng nhiệt độ của khí trong bình lên 1,8 lần

a) Tính nhiệt độ khí sau khi tăng.

b) Để áp suất của khí trong bình không đổi, người ta

#Vật lý lớp 10

2

NT

nguyễn thị hương giang

24 tháng 2 2022

$T_1=16^oC=16+273=289K$

Tăng nhiệt độ khí trong bình lên 1,8 lần thì:

$T_2=289\cdot1,8=520,2K$

Áp dụng quá trình đẳng áp:

$\dfrac{V_1}{T_1}=\dfrac{V_2}{T_2}$

$\Rightarrow\dfrac{20}{289}=\dfrac{V_2}{520,2}$

$\Rightarrow V_2=36l$

Đúng(6)

M

Minh3112jqka

24 tháng 2 2022

$T_{1} = 16^{o} C = 16 + 273 = 289 K$

Tăng nhiệt độ khí trong bình lên 1,8 lần thì:

$T_{2} = 289 \cdot 1, 8 = 520, 2 K$

Áp dụng quá trình đẳng áp:

$\frac{V_{1}}{T_{1}} = \frac{V_{2}}{T_{2}}$

$\Rightarrow \frac{20}{289} = \frac{V_{2}}{520, 2}$

$\Rightarrow V_{2} = 36 l$

Đúng(2)

SG

Sách Giáo Khoa

22 tháng 8 2017

Một bình chứa một lượng khí ở nhiệt độ 30^oC và áp suất 2 bar. (1 bar = 10⁵ Pa). Hỏi phải tăng nhiệt độ lên tới bao nhiêu độ để áp suất tăng gấp đôi?

#Vật lý lớp 10

1

AN

Ái Nữ

26 tháng 8 2017

Bài giải:

* Trạng thái 1: T₁ = 273 + 30 = 303 K

p₁ = 2 bar

* Trạng thái 2: T₂ = ? p₂ = 2p₁

* Vì thể tích bình không đổi nên:

$\dfrac{p_1}{T_1}=\dfrac{p_2}{T_2}\Rightarrow T_2=\dfrac{p_2.T_1}{p_1}=\dfrac{2p_1.T_1}{p_1}=2T_1=606k$

Đúng(0)

HD

Hoàng Đức Long

11 tháng 7 2017

Người ta điều chế khí hiđrô và chứa vào một bình lớn dưới áp suất 1 atm, ở nhiệt độ 20 ° C. Tính thể tích khí phải lấy từ bình lớn ra để nạp vào một bình nhỏ thể tích 20 lít dưới áp suất 25 atm. Coi nhiệt độ không đổi.

#Vật lý lớp 10

1

VT

Vũ Thành Nam

11 tháng 7 2017

V 1 = p 2 V 2 / p 1 = 25.20/1 = 500 lít

Đúng(0)

LH

Love Học 24

21 tháng 5 2016

Một bình chứa một lượng khí ở nhiệt độ 30 độ C và áp suất 2 bar ( 1 bar = 10⁵ Pa ) . Hỏi phải tăng nhiệt độ lên tới bao nhiêu độ để áp suất tăng gấp đôi.

#Vật lý lớp 10

2

YT

Yêu Tiếng Anh

21 tháng 5 2016

Ta có : T₁ = t^oC + 273 = 30 + 273 = 303^oK

p₁ = 2 bar = 2 . 10⁵ Pa

p₂ = 4 bar = 4 . 10⁵

Vì quá trình là đẳng tích , áp dụng định luật Charles ta có

$\frac{p_1}{p_2}=\frac{T_1}{T_2}$→ T₂ = $\frac{p_2.T_1}{p_1}=\frac{4.10^5.303}{2.10^5}$= 606^oK

Vậy để áp suất tăng lên gấp đôi , ta phải tăng nhiệt độ lên 606^oK

Đúng(0)

BN

bảo nam trần

21 tháng 5 2016

* Trạng thái 1: T₁ = 273 + 30 = 303 K

p₁ = 2 bar

* Trạng thái 2: T₂ = ? p₂ = 2p₁

* Vì thể tích bình không đổi nên:

$\frac{P1}{T1}=\frac{P2}{T2}\Rightarrow T2=\frac{P2.T1}{P1}=\frac{2P1.T1}{P1}$ = 2T₁= 606 K

Đúng(0)

J

jennifer

10 tháng 5 2022

Một cái bơm chứa 80cm3 không khí ở nhiệt độ 27 độ C và áp suất 10^5 Pa. Khi không khí nén xuống còn 20cm3 và nhiệt độ tăng lên tới 327 độ C thì áp suất của không khí trong bơm là?

#Vật lý lớp 10

1

C

☆Châuuu~~~(๑╹ω╹๑ )☆

10 tháng 5 2022

$\left\{{}\begin{matrix}p_1=10^5Pa\\V_1=80cm^3\\T_1=300^oK\end{matrix}\right.\\ \left\{{}\begin{matrix}p_2=?\\V_2=20cm^3\\T_2=600^oK\end{matrix}\right.\\ \dfrac{p_1V_1}{T_1}=\dfrac{p_2V_2}{T_2}\Leftrightarrow\dfrac{10^5.80}{300}=\dfrac{p_2.20}{600}\\ \Rightarrow p_2=8.10^5Pa$

Đúng(5)

NV

Nguyễn văn Quân

6 tháng 4 2021

Một cái bơm chứa 120cm3 không khí ở nhiệt độ 27độ c và áp suất 10^5 Pa. Khi không khí bị nén xuống còn 20cm3 và nhiệt độ tăng lên tới 327 độ c thì áp suất của không khí trong bơm là ?

#Vật lý lớp 10

2

Y

❤ ~~ Yến ~~ ❤

6 tháng 4 2021

T₁ = 27 + 273 = 300K

T₂ = 327 + 273 = 600K

Phương trình trạng thái khí lí tưởng:

$\dfrac{P_1V_1}{T_1}=\dfrac{P_2V_2}{T_2}\Rightarrow\dfrac{10^5.120}{300}=\dfrac{P_2.20}{600}\Leftrightarrow\dfrac{12000000}{300}=\dfrac{20P_2}{600}$

=> 20P₂ = 24000000

=> P₂ = 1200000Pa

Đúng(2)

S

Smile

6 tháng 4 2021

phương trình trạng thái lí tưởng:

$\dfrac{P_1.V_1}{T_1}=\dfrac{P_2.V_2}{T2}$

Theo đề bài:

V1 = 120cm3; T1 = 27 + 273 = 300K ; P1 = $10^5$Pa

V2 = 20cm3; T2 = 327 + 273 = 600K

Thay vào phương trình:

$\dfrac{10^5.120}{300}=\dfrac{P_2.20}{600}\Rightarrow P_2=\dfrac{P_1.T_2.V_2}{V_2.T_1}=1200000Pa$

=12.10^5 Pa

Đúng(0)

HD

Hoàng Đức Long

22 tháng 3 2017

Một bình kín có thể tích không đổi chứa khí lí tưởng ở áp suất 1,5. 10 5 Pa và nhiệt độ 20 ° C . Tính áp suất trong bình khi nhiệt độ trong bình tăng lên tới 40 ° C . A. p 2 = 1 , 6 . 10 6 P a . B. p 2 = 1 , 6 . 10 5 P a . C. p 2 = 1 , 6 . 10 7 ...

Đọc tiếp

#Vật lý lớp 10

1

VT

Vũ Thành Nam

22 tháng 3 2017

Đáp án: B

Vì thể tích của bóng đèn không đổi nên ta có:

p 1 T 1 = p 2 T 2 → p 2 = T 2 T 1 p 1 = 40 + 273 20 + 273 .1,5.10 5 = 1,6.10 5 (pa)

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP