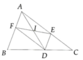
Cho tam giác ABC, điểm D thuộc cạnh BC. Đường thẳng qua D và song song với AC cắt AB tại E, đường thẳng qua D và song song với AB cắt AC tại F. Cho biết diện tích các tam giác EBD và FDC lần lượt bằng a 2 v à b 2 , hãy tính diện tích tam giác ABC.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
21 tháng 8 2017
Đúng(0)
Những câu hỏi liên quan
CM
11 tháng 12 2019
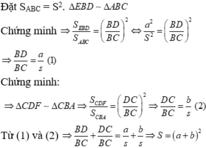
Đặt S A B C = S . Vì DE//AC nên Δ BED ∼ Δ BAC
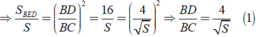
Lại có DF//AB nên Δ CDF ∼ Δ CBA
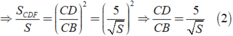
Cộng theo vế của đẳng thức ( 1 ) và ( 2 ) ta được:
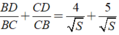
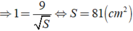
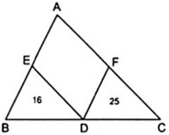
Vậy diện tích của tam giác ABC là 81 c m 2
H
30 tháng 11 2014
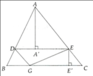
D là TĐ của AB mà DE //BC nên DE là đg TB của tam giác ABC -->E là TĐ của AC.
E là TĐ của AC mà EF //AB nên EF là đg TB của tam giác CAB--->F là TĐ của BC
CM
18 tháng 2 2019
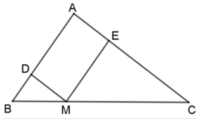
Ta có: MD // AC nên ΔDBM ~ ΔABC. Suy ra :
D B A B = B M B C = D M A C = D B + B M + D M A B + B C + C A
Do đó 1 3 = P B D M P A B C
Chu vi ΔDBM bằng 30. 1 3 = 10cm
Ta có ME // AB nên ΔEMC ~ ΔABC. Suy ra
E M A B = M C B C = E C A C = E M + M C + E C A B + B C + A C
do đó 2 3 = P E M C P A B C
Chu vi ΔEMC bằng 30. 2 3 = 20 cm
Vậy chu vi ΔDBM và chu vi ΔEMC lần lượt là 10cm; 20cm
Đáp án: D
CM
19 tháng 4 2017
Ta chứng minh được AEDF là hình bình hành Þ AD Ç È = I. I là trung điểm của AD và EF. Suy ra E đối xứng với F qua I
