Tập giá trị của x thỏa mãn:
x6 = 9.x4 là S={........}
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
22 tháng 12 2022
Lời giải:
$f(x)=m^2(x^4-1)+m(x^2-1)-6(x-1)=(x-1)[m^2(x+1)(x^2+1)+m(x+1)-6]$
Để $f(x)\geq 0$ với mọi $x\in\mathbb{R}$ thì:
$m^2(x+1)(x^2+1)+m(x+1)-6=Q(x)(x-1)^k$ với $k$ là số lẻ
$\Rightarrow h(x)=m^2(x+1)(x^2+1)+m(x+1)-6\vdots x-1$
$\Rightarrow h(1)=0$
$\Leftrightarrow 4m^2+2m-6=0$
$\Leftrightarrow 2m^2+m-3=0$
$\Leftrightarrow (m-1)(2m+3)=0\Rightarrow m=1$ hoặc $m=\frac{-3}{2}$
Thay các giá trị trên vào $f(x)$ ban đầu thì $m\in \left\{1; \frac{-3}{2}\right\}$
Tổng các giá trị của các phần tử thuộc $S$: $1+\frac{-3}{2}=\frac{-1}{2}$
LT
2
CM
27 tháng 2 2017
Chọn B.
Tiếp tuyến song song với trục Ox nên hệ số góc của tiếp tuyến bằng 0.
Do đó ta có
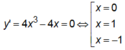
Với x = 0 thì phương trình tiếp tuyến y = m – 1009.
Với x = ± 1 thì phương trình tiếp tuyến y = m - 1010
Dễ thấy hai tiếp tuyến trên phân biệt nên để có đúng một tiếp tuyến song song với Ox thì có một tiếp tuyến trùng với Ox tức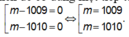 
Suy ra S = {1009;1010}
Vậy tổng các giá trị của S bằng 2019.