Question

[Pham Trong Bach]

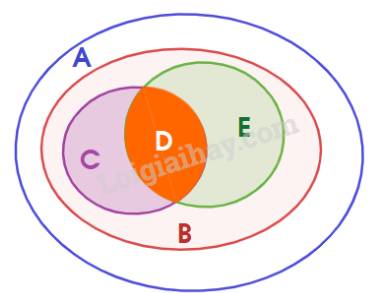
Cho A và B là hai tập hợp con của tập hợp E được biểu diễn bởi biểu đồ Ven dưới đây

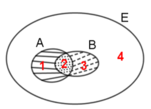
Trong các phát biểu sau

      I.            Vùng 1 là tập hợp A \ B.

     II.            Vùng 2 là tập hợp A ∩ B.

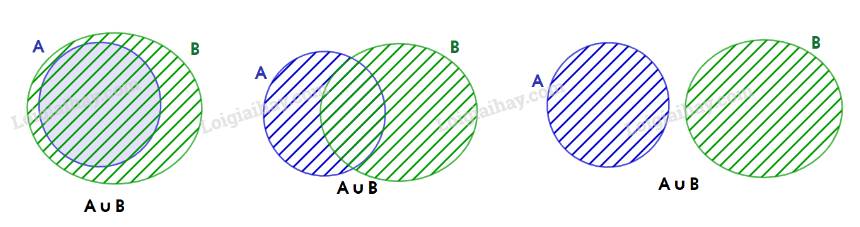
     III.            Vùng 3 là tập hợp B \ A.

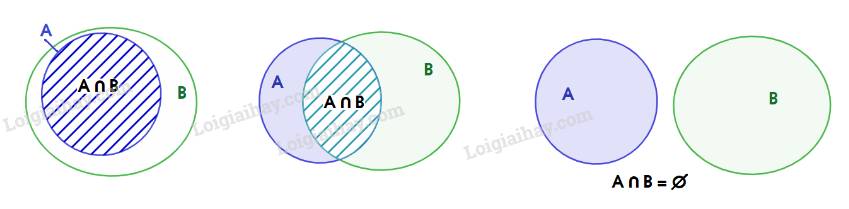
       IV.            Vùng 4 là tập hợp E \ (A ∪  B).

Số phát biểu đúng là:

A. 1.

B. 2.

C. 3.

D. 4.

Answer 1

[Cao Minh Tâm]

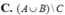
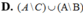
Đáp án: D

Nhìn vào hình vẽ ta thấy vùng 1 là tập hợp các phần tử thuộc A mà không thuộc B nên vùng 1 là A \ B;

Vùng 2 là tập hợp các phần tử vừa thuộc A vừa thuộc B nên vùng 2 là A ∩  B; Vùng 3 là tập hợp các phần tử thuộc B mà không thuộc A nên vùng 3 là B \ A; Vùng 4 là tập hợp các phần tử thuộc E mà không thuộc A; B nên vùng 4 là E \ (A ∪  B).

Vậy cả 4 phát biểu đều đúng