Tính giá trị biểu thức :(12-17).x khi x=2;x=4;x=6
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Khi tính giá trị của biểu thức có chứa dấu ( ) thì ta thực hiện các phép tính trong ngoặc trước.
b) Tính :
3 x (17 + 22) = 3 x 39 = 117
Giá trị của biểu thức 3 x (17 + 22) là 117.
(58 – 23) : 5 = 35 : 5 = 7.
Giá trị của biểu thức (58 – 23) : 5 = 7.
Với a = 8 thì giá trị của biểu thức 127 + 8 x 6 = 127 + 48 = 175

Khi \(x=2\), ta có:
\(\left(12-17\right).2\)
\(=\left(-5\right).2\)
\(=-10\)
Khi \(x=4\), ta có:
\(\left(12-17\right).4\)
\(=\left(-5\right).4\)
\(=-20\)
Khi \(x=6\), ta có:
\(\left(12-17\right).6\)
\(=\left(-5\right).6\)
\(=-30\)

x=11 suy ra 12=x+1 thay vào A ta có:
A=x^17- (x+1)x^16 + (x+1)x^15 - (x+1)x^14 + .....- (x+1)x^2+(x+1)x -1
= x^17 - x^17 -x^16 + x^16 + x^15 - x^15 - x^14 +.....- x^3 -x^2 + x^2 +x -1
= x-1= 11-1=10

\(E=\left(2x-5\right)^{10}-12\ge-12\)
Dấu "=" xảy ra \(\Leftrightarrow x=\dfrac{5}{2}\)
Vậy \(E_{min}=-12\Leftrightarrow x=\dfrac{5}{2}\)
\(F=\left(x+5\right)^8+\left|x+5\right|+22\ge22\)
Dấu "=" xảy ra \(\Leftrightarrow x=-5\)
Vậy \(F_{min}=22\Leftrightarrow x=-5\)
\(G=17-\left|3x-2\right|\)
Dấu "=" xảy ra \(x=\dfrac{2}{3}\)
Vậy \(G_{max}=17\Leftrightarrow x=\dfrac{2}{3}\)
\(K=17-\left|3x-2\right|-\left(2-3x\right)^{2020}\le17\)
Dấu "=" xảy ra \(\Leftrightarrow x=\dfrac{2}{3}\)
Vậy \(K_{max}=17\Leftrightarrow x=\dfrac{2}{3}\)

\(x=\sqrt[3]{3+2\sqrt{2}}+\sqrt[3]{3-2\sqrt{2}}\)
\(\Rightarrow x^3=3+2\sqrt{2}+3-2\sqrt{2}+3\sqrt[3]{\left(3+2\sqrt{2}\right)\left(3-2\sqrt{2}\right)}\left(\sqrt[3]{3+2\sqrt{2}}+\sqrt[3]{3-2\sqrt{2}}\right)\)
\(=6+3\sqrt[3]{9-8}.x=6+3x\)
\(\Rightarrow x^3-3x=6\)
\(y=\sqrt[3]{17+12\sqrt{2}}+\sqrt[3]{17-12\sqrt{2}}\)
\(\Rightarrow y^3=17+12\sqrt{2}+17-12\sqrt{2}+3\sqrt[3]{\left(17+12\sqrt{2}\right)\left(17-12\sqrt{2}\right)}\left(\sqrt[3]{17+12\sqrt{2}}+\sqrt[3]{17-12\sqrt{2}}\right)\)
\(=34+3\sqrt[3]{289-288}.y=34+3y\)
\(\Rightarrow y^3-3y=34\)
\(P=x^3+y^3-3\left(x+y\right)+2009=\left(x^3-3x\right)+\left(y^3-3y\right)+2009\)
\(=6+34+2009=2049\)

a: Khi x=9 thì \(A=\dfrac{17}{3+2}=\dfrac{17}{5}\)
b: 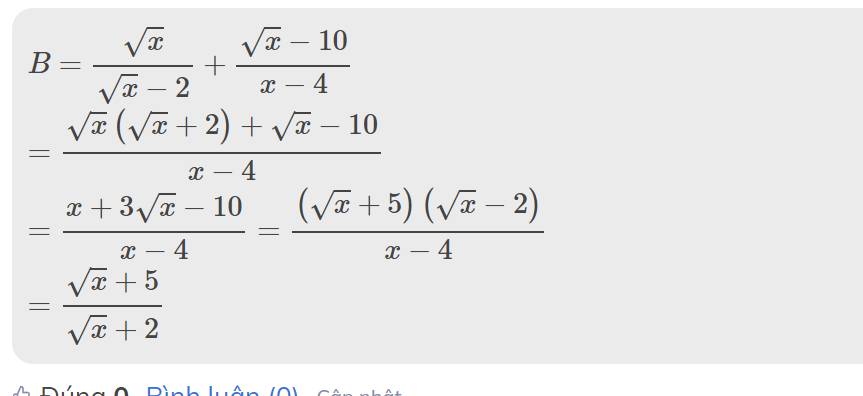
c: P=A:B
\(=\dfrac{17}{\sqrt{x}+2}:\dfrac{\sqrt{x}+5}{\sqrt{x}+2}=\dfrac{17}{\sqrt{x}+5}\)
Để P là số nguyên thì \(17⋮\sqrt{x}+5\)
mà \(\sqrt{x}+5>=5\) với mọi x thỏa mãn ĐKXĐ
nên \(\sqrt{x}+5=17\)
=>x=144

\(a,=\left(576-577\right)+\left(678-679\right)+\left(780-475\right)=-1-1+305=303\\ b,=158\times0=0\\ c,=12\left(36\times17\times34+15\right)=12\times20823=249876\)

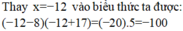
khi x=2
(12-17).2
=(-5).2
=-10
khi x=4
(12-17).4
=(-5).4
=-20
khi x=6
(12-17).6
=(-5).6
=-30