Giá trị nhỏ nhất của p;p+3;p+8 đều là các số chính phương
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TN
11 tháng 1 2017
bài này ko hay cho lắm, cách làm cụ thể nhất trong cái nhất r` đấy
a)Ta thấy: \(\left|x-5\right|\ge0\)
\(\Rightarrow-\left|x-5\right|\le0\)
\(\Rightarrow1000-\left|x-5\right|\le1000\)
\(\Rightarrow A\le1000\)
Dấu "=" xảy ra khi \(\left|x-5\right|=0\Leftrightarrow x=5\)
Vậy \(Max_A=1000\) khi \(x=5\)
b)Ta thấy: \(\left|y-3\right|\ge0\)
\(\Rightarrow\left|y-3\right|+50\ge50\)
\(\Rightarrow B\ge50\)
Dấu "="xảy ra khi \(\left|y-3\right|=0\Leftrightarrow y=3\)
Vậy \(Min_B=50\) khi \(y=3\)
c)Ta thấy: \(\hept{\begin{cases}\left|x-100\right|\ge0\\\left|y+200\right|\ge0\end{cases}}\)
\(\Rightarrow\left|x-100\right|+\left|y+200\right|\ge0\)
\(\Rightarrow\left|x-100\right|+\left|y+200\right|-1\ge-1\)
\(\Rightarrow C\ge-1\)
Dấu "=" xảy ra khi \(\hept{\begin{cases}\left|x-100\right|=0\\\left|y+200\right|=0\end{cases}}\Rightarrow\hept{\begin{cases}x=100\\y=-200\end{cases}}\)
Vậy \(Min_C=-1\) khi \(\hept{\begin{cases}x=100\\y=-200\end{cases}}\)
AH
Akai Haruma
Giáo viên
3 tháng 2 2024
Câu 1:
$y=-2x^2+4x+3=5-2(x^2-2x+1)=5-2(x-1)^2$
Vì $(x-1)^2\geq 0$ với mọi $x\in\mathbb{R}$ nên $y=5-2(x-1)^2\leq 5$
Vậy $y_{\max}=5$ khi $x=1$
Hàm số không có min.
AH
Akai Haruma
Giáo viên
3 tháng 2 2024
Câu 2:
Hàm số $y$ có $a=-3<0; b=2, c=1$ nên đths có trục đối xứng $x=\frac{-b}{2a}=\frac{1}{3}$
Lập BTT ta thấy hàm số đồng biến trên $(-\infty; \frac{1}{3})$ và nghịch biến trên $(\frac{1}{3}; +\infty)$
Với $x\in (1;3)$ thì hàm luôn nghịch biến
$\Rightarrow f(3)< y< f(1)$ với mọi $x\in (1;3)$
$\Rightarrow$ hàm không có min, max.
11 tháng 7 2019
a) Ta có: \(\left|x+\frac{3}{2}\right|\ge0\forall x\)
Hay : P \(\ge\)0 \(\forall\)x
Dấu "=" xảy ra khi: \(x+\frac{3}{2}=0\) <=> \(x=-\frac{3}{2}\)
Vậy Pmin = 0 tại x = -3/2
b) Ta có: \(\left|3-x\right|\ge0\forall x\)
=> \(\left|3-x\right|+\frac{2}{5}\ge\frac{2}{5}\forall x\)
hay P \(\ge\)2/5 \(\forall\)x
Dấu "=" xảy ra khi: 3 - x = 0 <=> x = 3
Vậy Pmin = 2/5 tại x = 3
11 tháng 7 2019
a)Có giá trị tuyệt đối của x+3/2 >=0 với mọi x
=> P>=0 với mọi x
P=0 khi x+3/2=0 <=> x=-3/2
Vậy P có giá trị nhỏ nhất là 0 khi x=-3/2
5 tháng 2 2021
1, Ta có: 3-x2+2x=-(x2-2x+1)+4=-(x-1)2+4
vì (x-1)2 luôn lớn hơn hoặc bằng không với mọi x-->-(x-1)2 nhỏ hơn hoặc bằng 0 với mọi x
vậy giá trị lớn nhất của biểu thức 3-x2+2x là 4
5 tháng 2 2021
các bài giá trị nhỏ nhất còn lại làm tương tự bạn nhé
chỉ cần đưa về nhân tử chung hoặc hằng đẳng thức là được
YN
30 tháng 6 2021
\(1.\)
\(-17-\left(x-3\right)^2\)
Ta có: \(\left(x-3\right)^2\ge0\)với \(\forall x\)
\(\Leftrightarrow-\left(x-3\right)^2\le0\)với \(\forall x\)
\(\Leftrightarrow17-\left(x-3\right)^2\le17\)với \(\forall x\)
Dấu '' = '' xảy ra khi:
\(\left(x-3\right)^2=0\)
\(\Leftrightarrow x-3=0\)
\(\Leftrightarrow x=3\)
Vậy \(Max=-17\)khi \(x=3\)
YN
30 tháng 6 2021
\(2.\)
\(A=x\left(x+1\right)+\frac{3}{2}\)
\(A=x^2+x+\frac{3}{2}\)
\(A=\left(x+\frac{1}{2}\right)^2+\frac{5}{4}\)
\(\left(x+\frac{1}{2}\right)^2+\frac{5}{4}\ge\frac{5}{4}\)với \(\forall x\)
\(\Leftrightarrow\left(x+\frac{1}{2}\right)^2+\frac{5}{4}\ge\frac{5}{4}\)với \(\forall x\)
Vậy \(Max=\frac{5}{4}\)khi \(x=\frac{-1}{2}\)
AH
Akai Haruma
Giáo viên
12 tháng 11 2023
Lời giải:
a. ĐKXĐ: $x\geq 0; x\neq 1$
\(P=\frac{x\sqrt{x}+26\sqrt{x}-19}{(\sqrt{x}-1)(\sqrt{x}+3)}-\frac{2\sqrt{x}(\sqrt{x}+3)}{(\sqrt{x}-1)(\sqrt{x}+3)}+\frac{(\sqrt{x}-3)(\sqrt{x}-1)}{(\sqrt{x}+3)(\sqrt{x}-1)}\)
\(=\frac{x\sqrt{x}+26\sqrt{x}-19-(2x+6\sqrt{x})+(x-4\sqrt{x}+3)}{(\sqrt{x}+3)(\sqrt{x}-1)}\\ =\frac{x\sqrt{x}+16\sqrt{x}-x-16}{(\sqrt{x}+3)(\sqrt{x}-1)}\\ =\frac{(x+16)(\sqrt{x}-1)}{(\sqrt{x}-1)(\sqrt{x}+3)}=\frac{x+16}{\sqrt{x}+3}\)
b.
$P=\frac{x+16}{\sqrt{x}+3}=\frac{(x-9)+25}{\sqrt{x}+3}$
$=(\sqrt{x}-3)+\frac{25}{\sqrt{x}+3}=(\sqrt{x}+3)+\frac{25}{\sqrt{x}+3}-6$
$\geq 2\sqrt{25}-6=4$ (áp dụng BĐT Cô-si)
Vậy $P_{\min}=4$. Giá trị này đạt tại $\sqrt{x}+3=\frac{25}{\sqrt{x}+3}\Leftrightarrow x=4$
DT
11 tháng 4 2020
C=a2-4ab+4b2+b2-2b+1-7=(a-2b)2+(b-1)2-7 > hoặc =-7
dấu = xảy ra khi a-2b=0
b-1=0
<=>a=2;b=1
..................................
4 tháng 5 2023
program TimMinMaxTrungBinh;
var
N, i, max, min, sum: integer;
a: array[1..50] of integer;
TB, minTB, maxTB: real;
begin
writeln('Nhap so nguyen duong N:');
readln(N);
sum := 0;
for i := 1 to N do
begin
write('Nhap so thu ', i, ': ');
readln(a[i]);
sum := sum + a[i];
end;
max := a[1];
min := a[1];
for i := 2 to N do
begin
if a[i] > max then
max := a[i];
if a[i] < min then
min := a[i];
end;
TB := sum / N;
minTB := TB;
maxTB := TB;
for i := 1 to N do
begin
if (a[i] < TB) and (a[i] < minTB) then
minTB := a[i];
if (a[i] > TB) and (a[i] > maxTB) then
maxTB := a[i];
end;
writeln('Gia tri lon nhat la: ', max);
writeln('Gia tri nho nhat la: ', min);
writeln('Gia tri trung binh la: ', TB:2:2);
if minTB = TB then
writeln('Khong co gia tri nao nho hon TB')
else
writeln('Gia tri nho nhat < TB la: ', minTB);
if maxTB = TB then
writeln('Khong co gia tri nao lon hon TB')
else
writeln('Gia tri lon nhat > TB la: ', maxTB);
readln;
end.
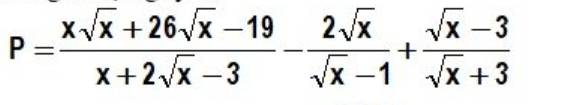
Với p = 1 => p = 1 là số chính phương
p + 3 = 4 là số chính phương
p + 8 = 9 là số chính phương
Vậy pmin = 1
p = 1 , tich minh nha Mori Ran