Một con lắc lò xo treo thẳng đứng dao động điều hòa với chu kỳ 1 s, sau 2,5 s kể từ lúc bắt đầu dao động vật có li độ - 5 2 cm đi theo chiều âm với tốc độ 10 π 2 cm/s. Chọn trục tọa độ Ox thẳng đứng, gốc tọa độ tại vị trí cân bằng và chiều dương hướng xuống. Biết lực đàn hồi của lò xo nhỏ nhất 6 N. Lấy g = π 2 Lực đàn hồi của lò xo tác dụng vào vật lúc t = 0 là
A. 12,28 N.
B. 7,2 N.
C. 8,17 N.
D. 12,82 N.


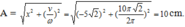

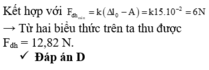


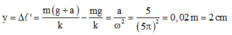
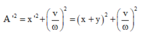
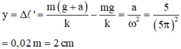
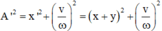

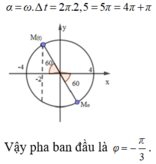
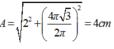
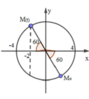
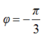
Chọn D.