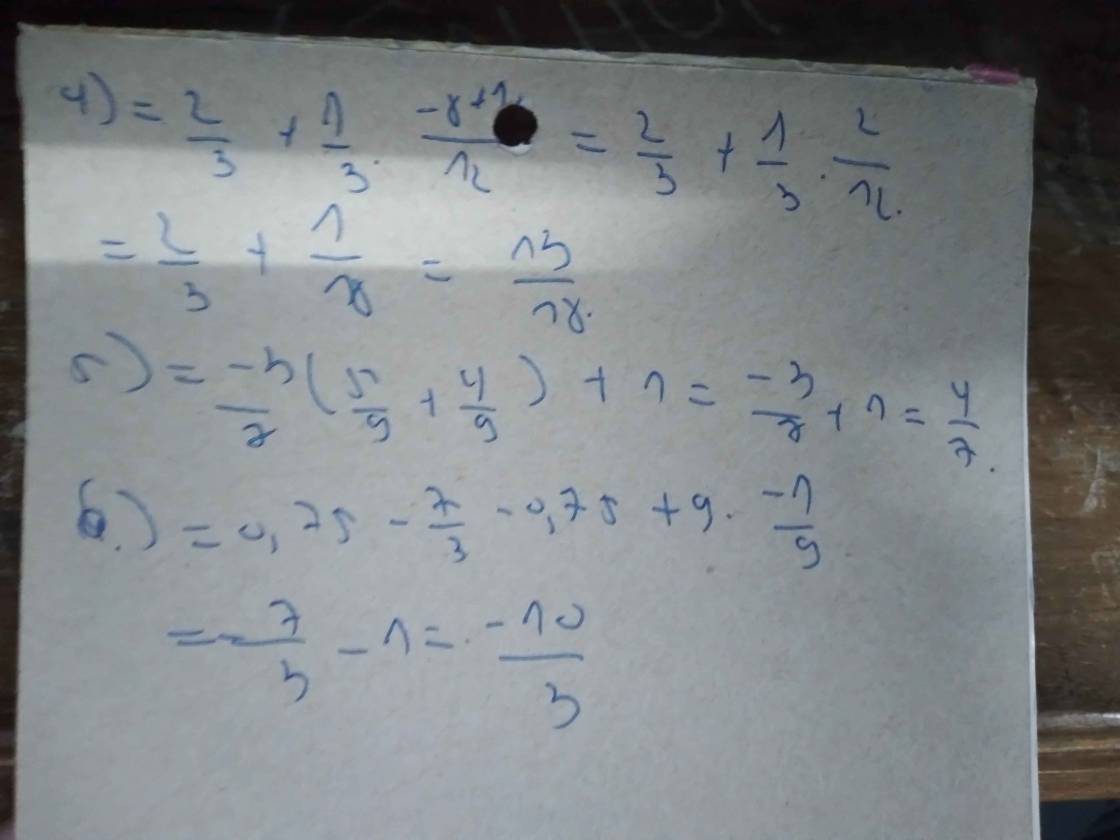Thực hiện các phép tính: 3 x - 5 x - 3 - 3 x 2 + 1 x 2 - 9
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
5 tháng 9 2018
Đúng(0)
Những câu hỏi liên quan
7 tháng 1 2022
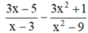
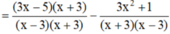
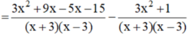
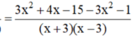
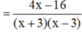
Bài 1:
b: \(=\dfrac{x+3-4-x}{x-2}=\dfrac{-1}{x-2}\)
Bài 2:
a: \(=\dfrac{x+1}{2\left(x+3\right)}+\dfrac{2x+3}{x\left(x+3\right)}\)
\(=\dfrac{x^2+x+4x+6}{2x\left(x+3\right)}=\dfrac{x^2+5x+6}{2x\left(x+3\right)}=\dfrac{x+2}{2x}\)
d: \(=\dfrac{3}{2x^2y}+\dfrac{5}{xy^2}+\dfrac{x}{y^3}\)
\(=\dfrac{3y^2+10xy+2x^3}{2x^2y^3}\)
e: \(=\dfrac{x^2+2xy+x^2-2xy-4xy}{\left(x+2y\right)\left(x-2y\right)}=\dfrac{2x^2-4xy}{\left(x+2y\right)\cdot\left(x-2y\right)}=\dfrac{2x}{x+2y}\)
13 tháng 5 2023
2:
a: =>-2x=10
=>x=-5
b: =>(x-3)(2x+5)=0
=>x=3 hoặc x=-5/2
31 tháng 3 2021
Bài 1:
a) Ta có: \(\dfrac{2}{5}\cdot x+\dfrac{1}{3}=\dfrac{1}{5}\)
\(\Leftrightarrow\dfrac{2}{5}\cdot x=\dfrac{1}{5}-\dfrac{1}{3}=\dfrac{-2}{15}\)
\(\Leftrightarrow x=\dfrac{-2}{15}:\dfrac{2}{5}=\dfrac{-2}{15}\cdot\dfrac{5}{2}\)
hay \(x=-\dfrac{1}{3}\)
Vậy: \(x=-\dfrac{1}{3}\)
b) Ta có: \(\dfrac{1}{5}+\dfrac{5}{3}:x=\dfrac{1}{2}\)
\(\Leftrightarrow\dfrac{5}{3}:x=\dfrac{1}{2}-\dfrac{1}{5}=\dfrac{3}{10}\)
\(\Leftrightarrow x=\dfrac{5}{3}:\dfrac{3}{10}=\dfrac{5}{3}\cdot\dfrac{10}{3}\)
hay \(x=\dfrac{50}{9}\)
Vậy: \(x=\dfrac{50}{9}\)
c) Ta có: \(\dfrac{4}{9}-\dfrac{5}{3}\cdot x=-2\)
\(\Leftrightarrow\dfrac{5}{3}x=\dfrac{4}{9}+2=\dfrac{22}{9}\)
\(\Leftrightarrow x=\dfrac{22}{9}:\dfrac{5}{3}=\dfrac{22}{9}\cdot\dfrac{3}{5}\)
hay \(x=\dfrac{22}{15}\)
Vậy: \(x=\dfrac{22}{15}\)
d) Ta có: \(\dfrac{5}{7}:x-3=\dfrac{-2}{7}\)
\(\Leftrightarrow\dfrac{5}{7}:x=\dfrac{-2}{7}+3=\dfrac{19}{21}\)
\(\Leftrightarrow x=\dfrac{5}{7}:\dfrac{19}{21}=\dfrac{5}{7}\cdot\dfrac{21}{19}\)
hay \(x=\dfrac{15}{19}\)
Vậy:\(x=\dfrac{15}{19}\)
LT
3
6 tháng 8 2020
\(\frac{4}{x-3}+\frac{5}{x+3}-\frac{13-9x^2}{x^2-9}\)
ĐKXĐ : \(x\ne\pm3\)
\(=\frac{4}{x-3}+\frac{5}{x+3}-\frac{13-9x^2}{\left(x+3\right)\left(x-3\right)}\)
\(=\frac{4\left(x+3\right)}{\left(x+3\right)\left(x-3\right)}+\frac{5\left(x-3\right)}{\left(x+3\right)\left(x-3\right)}-\frac{13-9x^2}{\left(x+3\right)\left(x-3\right)}\)
\(=\frac{4x+12}{\left(x+3\right)\left(x-3\right)}+\frac{5x-15}{\left(x+3\right)\left(x-3\right)}-\frac{13-9x^2}{\left(x+3\right)\left(x-3\right)}\)
\(=\frac{4x+12+5x-15-13+9x^2}{\left(x+3\right)\left(x-3\right)}\)
\(=\frac{9x^2+9x-16}{\left(x+3\right)\left(x-3\right)}=\frac{9x^2+9x-16}{x^2-9}\)
16 tháng 3 2017
Ta có : 1x2x3x...x9-1x2x3x...x8-1x2x3x...x8^2
=1x2x3x...x8x(9-1-8)
=1x2x3x...x8x0
=0
Nhớ k cho mik nha !!!
TM
21 tháng 12 2021
a/ \(\left(2x+3\right)\left(x-5\right)-\left(x-1\right)^2+x\left(7-x\right)\)
\(=2x^2-2x-15-x^2+2x-1+7x-x^2\)
\(=7x-16\)
AD
23 tháng 7 2023
\(a,\dfrac{x^2-9}{x-2}:\dfrac{x-3}{x}\\ =\dfrac{\left(x-3\right)\left(x+3\right)}{x-2}\times\dfrac{x}{x-3}\\ =\dfrac{x\left(x+3\right)}{\left(x-2\right)}\)
\(b,\dfrac{x}{z^2}.\dfrac{xz}{y^3}:\dfrac{x^3}{yz}\\ =\dfrac{x}{z^2}.\dfrac{xz}{y^3}.\dfrac{yz}{x^3}=\dfrac{x^2yz^2}{z^2y^3x^3}=\dfrac{1}{xy^2}\)
\(c,\dfrac{2}{x}-\dfrac{2}{x}:\dfrac{1}{x}+\dfrac{4}{x}.\dfrac{x^2}{2}\\ =\dfrac{2}{x}-\dfrac{2}{x}\times\dfrac{x}{1}+\dfrac{4x^2}{2x}\\ =\dfrac{2}{x}-\dfrac{2}{1}+2x\\ =\dfrac{2-2x+2x^2}{x}\)
H9
HT.Phong (9A5)
CTVHS
23 tháng 7 2023
a) \(\dfrac{x^2-9}{x-2}:\dfrac{x-3}{x}\)
\(=\dfrac{\left(x+3\right)\left(x-3\right)}{x-2}\cdot\dfrac{x}{x-3}\)
\(=\dfrac{x\left(x+3\right)}{x-2}\)
b) \(\dfrac{x}{z^2}\cdot\dfrac{xz}{y^3}:\dfrac{x^3}{yz}\)
\(=\dfrac{x}{z^2}\cdot\dfrac{xz}{y^3}\cdot\dfrac{yz}{x^3}\)
\(=\dfrac{1}{xy^2}\)
c) \(\dfrac{2}{x}-\dfrac{2}{x}:\dfrac{1}{x}+\dfrac{4}{x}\cdot\dfrac{x^2}{2}\)
\(=\dfrac{2}{x}-\dfrac{2}{x}\cdot x+\dfrac{4}{x}\cdot\dfrac{x^2}{2}\)
\(=\dfrac{2}{x}\cdot\left(1-x+2\right)\)
\(=\dfrac{2}{x}\cdot\left(3-x\right)\)
\(=\dfrac{6}{x}-2\)
11 tháng 12 2020
a) ( 3 + x )2 = x2 + 6x + 9
b) ( 5 - x )3 = 125 - 75x + 45x2 - x3
c) ( 2x - 1 )( x2 - x + 3 ) = 2x3 - 2x2 + 6x - x2 + x - 3 = 2x3 - 3x2 + 7x - 3
d) \(\frac{9}{x^2+3x}-\frac{3-x}{x}=\frac{9}{x\left(x+3\right)}+\frac{x-3}{x}\)
\(=\frac{9}{x\left(x+3\right)}+\frac{\left(x-3\right)\left(x+3\right)}{x\left(x+3\right)}\)
\(=\frac{9+x^2-9}{x\left(x+3\right)}=\frac{x^2}{x\left(x+3\right)}=\frac{x}{x+3}\)
11 tháng 12 2020
a, \(\left(3+x\right)^2=9+6x+x^2\)
b, \(\left(5-x\right)^3=125-75x+15x^2-x^3\)
c, \(\left(2x-1\right)\left(x^2-x+3\right)=2x^3-2x^2+6x-x^2+x-3=2x^3-3x^2+7x-3\)
d, \(\frac{9}{x^2+3x}-\frac{3-x}{x}=\frac{9}{x\left(x+3\right)}-\frac{3-x}{x}=\frac{9}{x\left(x+3\right)}+\frac{\left(x-3\right)\left(x+3\right)}{x\left(x+3\right)}\)
\(=\frac{9+x^2-9}{x\left(x+3\right)}=\frac{x^2}{x\left(x+3\right)}\)