Tính tổng S =
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét khai triển:
\(\left(1+x\right)^n=C_n^0+xC_n^1+x^2C_n^2+...+x^nC_n^n\)
Đạo hàm 2 vế:
\(n\left(1+x\right)^{n-1}=C_n^1+2xC_n^2+...+n.x^{n-1}C_n^n\)
Thay \(x=1\)
\(\Rightarrow n.2^{n-1}=C_n^1+2C_n^2+...+nC_n^n\)
\(\Rightarrow n.2^{n-1}+1=C_n^0+C_n^1+2C_n^2+...+nC_n^n\)
\(\Rightarrow S=n.2^{n-1}+1\)

Xét khai triển:
\(\left(1+x\right)^n=C_n^0+xC_n^1+x^2C_n^2+...+x^nC_n^n\)
Đạo hàm 2 vế:
\(n\left(1+x\right)^{n-1}=C_n^1+2xC_n^2+...+nx^{n-1}C_n^n\)
Tiếp tục đạo hàm 2 vế:
\(\left(n-1\right)n\left(1+x\right)^{n-2}=2C_n^2+2.3xC_n^3+...+\left(n-1\right)nx^{n-2}C_n^n\)
Thay \(x=1\)
\(\Rightarrow\left(n-1\right)n.2^{n-2}=1.2C_n^2+2.3C_n^3+...+\left(n-1\right)nC_n^n\)
\(\Rightarrow\left(n-1\right)n.2^{n-2}+n=C_n^1+1.2C_n^2+...+\left(n-1\right)n.C_n^n\)
\(\Rightarrow S=\left(n-1\right)n.2^{n-2}+n\)

\(lim\left(\frac{3n+2}{n+2}+a^2-4a\right)=lim\left(\frac{3+\frac{2}{n}}{1+\frac{2}{n}}+a^2-4a\right)=a^2-4a+3\)
\(\Rightarrow a^2-4a+3=0\Rightarrow\left[{}\begin{matrix}a=1\\a=3\end{matrix}\right.\)
\(\Rightarrow S=4\)
Khai triển nhị thức Niutơn của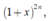 ta có
ta có
Cho x = 1, ta được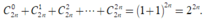
Chọn A.