Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B. Biết SA vuông góc với mặt phẳng (ABC),
A
B
=
a
,
B
C
=
a
3
,
S
A
=
a
. Một mặt phẳng
α
qua A vuông góc SC tại H và cắt SB tại K. Tính thể tích khối chóp S.AHK theo a A.
V
S
.
A
H
K
=
a
3
3
20
B.
V
S
.
A
H
K
=
...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B. Biết SA vuông góc với mặt phẳng (ABC), A B = a , B C = a 3 , S A = a . Một mặt phẳng α qua A vuông góc SC tại H và cắt SB tại K. Tính thể tích khối chóp S.AHK theo a
A. V S . A H K = a 3 3 20
B. V S . A H K = a 3 3 30
C. V S . A H K = a 3 3 60
D. V S . A H K = a 3 3 90
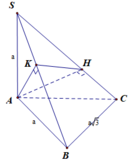
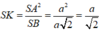
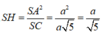
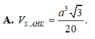
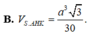
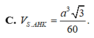
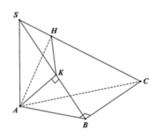
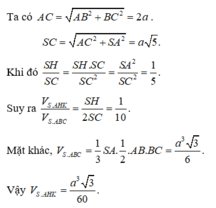
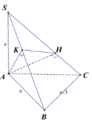
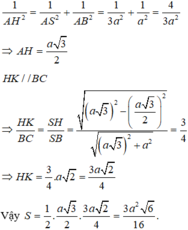
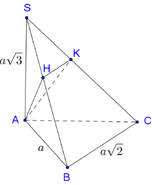
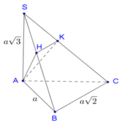
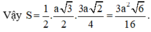
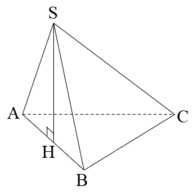
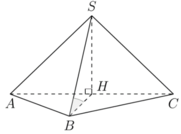
Ta có A K ⊥ S C A K ⊥ α A K ⊥ B C B C ⊥ S A B
Suy ra A K ⊥ S B C ⇒ A K ⊥ S B .
Vì ∆ S A B vuông cân tại A nên K là trung điểm của SB. Ta có
V S . A H K V S . A B C = S A . S K . S H S A . S B . S C = S H 2 S C
Ta có
A V = A B 2 + B C 2 = 2 a S V = A C 2 + S A 2 = a 5 .
Khi đó S H S C = S H . S C S C 2 = S A 2 S C 2 = 1 5
Suy ra V S . A H K V S . A B C = S H 2 S C = 1 10
Mặt khác V S . A B C = 1 3 S A . 1 2 A B . B C = a 3 3 6 Vậy V S . A H K = a 3 3 60
Đáp án C