Cho đường tròn (C) và điểm A nằm ngoài mặt phẳng chứa (C). Có tất cả bao nhiêu mặt cầu chứa đường tròn (C) và đi qua A?
A. 0 B. 1
C. 2 D. Vô số
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
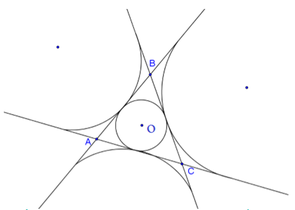
Ba điểm A,B,C tạo thành một tam giác. Có 4 đường tròn tiếp xúc với cả ba đường thẳng AB,AC,BC (hình vẽ trên).
Mặt cầu (S) cần tìm tiếp xúc với 3 đường thẳng AB,AC,BC, do đó nó phải chứa 1 trong 4 đường tròn trên.
Xét với 1 đường tròn bất kì trong 4 đường tròn trên, giả sử là đường tròn tâm (O) nằm bên trong tam giác, ta có:
Tâm I của mặt cầu (S) phải nằm trên đường thẳng d đi qua tâm O và vuông góc với (ABC). Mặt khác, I thuộc mp (P) chứa (C), (C) lại không vuông góc với (ABC) do đó chỉ có 1 giao điểm của d với (P). Tương tự, với 3 đường tròn còn lại, với mỗi đường tròn ta tìm được 1 tâm I nữa. Vậy có 4 mặt cầu thỏa mãn yêu cầu.

a: góc OHK+góc OBK=180 độ
=>OHKB nội tiếp
b: góc AHK=góc AOK
góc BHK=góc BOK
mà góc AOK=góc BOK
nên góc AHK=góc BHK
=>HK là phân giác của góc AHB

a: Xét tứ giác CMON có \(\widehat{CMO}+\widehat{CNO}=90^0+90^0=180^0\)
nên CMON là tứ giác nội tiếp
=>C,M,O,N cùng thuộc một đường tròn
b: Xét (O) có
\(\widehat{CMA}\) là góc tạo bởi tiếp tuyến MC và dây cung MA
\(\widehat{ABM}\) là góc nội tiếp chắn cung AM
Do đó: \(\widehat{CMA}=\widehat{ABM}=\widehat{CBM}\)
Xét ΔCMA và ΔCBM có
\(\widehat{CMA}=\widehat{CBM}\)
\(\widehat{MCA}\) chung
Do đó: ΔCMA~ΔCBM
=>\(\dfrac{CM}{CB}=\dfrac{CA}{CM}\)
=>\(CM^2=CA\cdot CB\)
c: Xét (O) có
CM,CN là các tiếp tuyến
Do đó: CM=CN
=>C nằm trên đường trung trực của MN(1)
Ta có: OM=ON
=>O nằm trên đường trung trực của MN(2)
Từ (1),(2) suy ra OC là đường trung trực của MN
=>OC\(\perp\)MN tại H
Xét ΔCMO vuông tại M có MH là đường cao
nên \(CH\cdot CO=CM^2\)
=>\(CH\cdot CO=CA\cdot CB\)
=>\(\dfrac{CH}{CB}=\dfrac{CA}{CO}\)
Xét ΔCHA và ΔCBO có
\(\dfrac{CH}{CB}=\dfrac{CA}{CO}\)
\(\widehat{HCA}\) chung
Do đó: ΔCHA~ΔCBO
=>\(\widehat{CHA}=\widehat{CBO}\)
mà \(\widehat{CBO}=\widehat{OAB}\)(ΔOAB cân tại O)
nên \(\widehat{CHA}=\widehat{OAB}\)
Chọn B.
(h.11) Lấy điểm M 0 cố định trên đường tròn (C).
Gọi ( α ) là mặt phẳng trung trực của A M 0 và đường thẳng Δ là trục của (C)
Ta có: I = ( α ) ∩ ∆ là tâm mặt cầu thỏa mãn yêu cầu đề bài.
Nhận xét: Tâm I là duy nhất. Thật vậy, giả sử M nằm trên đường tròn (C) khác với M 0
Gọi ( α ') là mặt phẳng trung trực của AM và I' = ( α ') ∩ ∆
Khi đó, mặt cầu tâm I' thỏa mãn yêu cầu đề bài.
Ta có: I'A = I'M = I' M 0 cho ta I' thuộc mặt phẳng trung trực (α) của A M 0
Suy ra: I' = (α) ∩ ∆
Vậy I' ≡ I