Cho hai phương trình: x 2 - 2 m x + 1 = 0 và x 2 - 2 x + m = 0 . Gọi S là tập hợp các giá trị của mm để mỗi nghiệm của phương trình này là nghịch đảo của một nghiệm của phương trình kia. Tổng các phần tử của S gần nhất với số nào dưới đây?
A. -1
B. 0
C. 1
D. Một đáp số khác


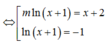
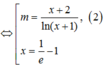

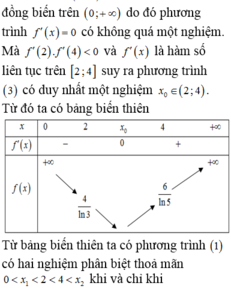
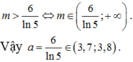


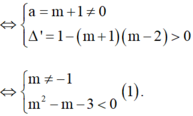
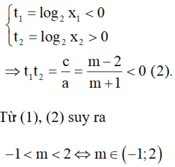
Gọi x 1 , x 2 là nghiệm của phương trình x 2 - 2 m x + 1 = 0 . Khi đó x 1 + x 2 = 2 m x 1 . x 2 = 1
Gọi x 3 , x 4 là nghiệm của phương trình x 2 - 2 m x + 1 = 0 . Khi đó x 3 + x 4 = 2 x 3 . x 4 = m
Ta có: x 1 = 1 x 3 x 2 = 1 x 4 ⇒ x 1 + x 2 = 1 x 3 + 1 x 4 x 1 . x 2 = 1 x 3 . x 4
⇒ x 1 + x 2 = x 3 + x 4 x 3 . x 4 x 1 . x 2 = 1 x 3 . x 4 ⇔ 2 m = 2 m 1 = 1 m ⇔ m = 1
Đáp án cần chọn là: C