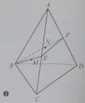
Cho tứ diện đều ABCD có cạnh bằng a. Gọi G là trọng tâm tam giác ABC. Mặt phẳng (GCD) cắt tứ diện theo 1 thiết diện có diện tích là
A. a 2 3 2 .
B. a 2 2 4 .
C. a 2 2 6 .
D. a 2 4 4 .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
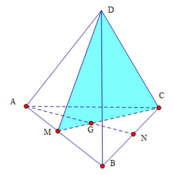
Thiết diện là tam giác cân MCD trong đó M là trung điểm AB n
Ta có D M = C M = a 3 2 ; C D = a
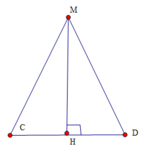
Gọi H là trung điểm
C D ⇒ M H = M C 2 − C H 2 = 3 a 2 4 − a 2 4 = a 2 2
S M C D = 1 2 M H . C D = 1 2 a 2 2 . a = a 2 2 4

Đáp án D
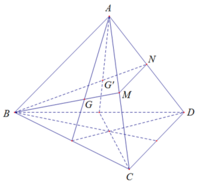
Trong(ABC), ta có: BG cắt AC tại M
Trong (ABD), ta có: BG’ cắt AD tại N
⇒ (BGG’) ∩ (ACD) = MN
Thiết diện cần tìm là (BMN)
Xét tam giác BMN có:
MN = 1 2 CD = a 2 ( MN là đường trung bình của tam giác ACD)
BM = BN = a 3 2 (BM, BN lần lượt là đường trung tuyến của tam giác ABC, ABD)
Áp dụng công thức heron:
S = p p - a p - b p - c = a 2 11 6

Đáp án D
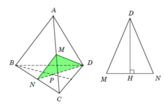
Trong tam giác BCD có: P là trọng tâm, N là trung điểm BC . Suy ra N , P , D thẳng hàng.
Vậy thiết diện là tam giác MND .
Xét tam giác MND , ta có ![]()
![]()
Do đó tam giác MND cân tại D .
Gọi H là trung điểm MN suy ra DH ⊥ MN
Diện tích tam giác ![]()
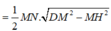
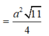

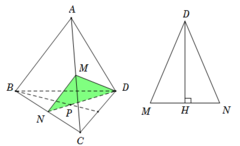
Trong tam giác BCD có: Plà trọng tâm, N là trung điểm BC .
Suy ra N; P; D thẳng hàng.
Vậy thiết diện là tam giác MND..
Xét tam giác MND, ta có M N = A B 2 = a ; D M = D N = A D 3 2 = a 3
Do đó tam giác MND cân tại D.
Gọi H là trung điểm MN suy ra DH và MN vuông góc với nhau..
Diện tích tam giác S Δ M N D = 1 2 M N . D H = 1 2 M N . D M 2 − M H 2 = a 2 11 4
Chọn C.

Trong (ABD), BN cắt AD tại F. Trong (ABC), BM cắt AC tại E.
Do M, N lần lượt là trọng tâm của ∆ABC và ∆ABD nên E, F lần lượt là trung điểm của AC, AD
Tứ diện ABCD có cạnh bằng a nên BE = BF = (a√3)/2
Thiết diện là tam giác cân BEF tại B, có đay EF = a/2
Diện tích BEF là
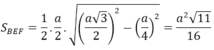
Đáp án D
Gọi M; N lần lượt là trung điểm của AB và B C suy ra AN và MC cắt nhau tại G
Dễ thấy mặt phẳng (GCD) cắt đường thắng AB tại điểm M.
Suy ra tam giác MCD là thiết diện của mặt phẳng (GCD) và tứ diện.
Tam giác ABD đều, có M là trung điểm AB suy ra
Tam giác A BC đều, có
Chọn B.