làm giúp em nha mọi người , chỉ cần làm bài 5 thôi ạ :
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


BT4: Hiệu suất phản ứng:
\(H=\dfrac{m_{tt}}{m_{lt}}.100\%=\dfrac{36,48}{48}.100\%=76\%\)
BT5 Khối lượng đồng thu được:
\(H=\dfrac{m_{tt}}{m_{lt}}.100\%\Rightarrow m_{tt}=\dfrac{m_{lt}.H}{100\%}=\dfrac{48.95}{100\%}=45,6\left(g\right)\)

24 B
25 C
26 B
27 C
28 A
29 D
30 C
31 A
32 C
33 B
34 B
35 D
36 C
37 C
38 B
39 C

1.A 2.B 3. D 4. C 5.B 6. A 7. D 8. C 9. D 10. B
11 B 12 D 13 C 14 A 15 C 16 A 17 D 18 B 19 B 20 C
21 A
22 A

Bài 6:
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{41}=\dfrac{b}{29}=\dfrac{c}{30}=\dfrac{a+b}{41+29}=\dfrac{700}{70}=10\)
Do đó: a=410; b=290; c=300

11 c)
\(a^2+2\ge2\sqrt{a^2+1}\Leftrightarrow a^2+1-2\sqrt{a^2+1}+1\ge0\Leftrightarrow\left(\sqrt{a^2+1}-1\right)^2\ge0\) (luôn đúng)
12 a) Có a+b+c=1\(\Rightarrow\) (1-a)(1-b)(1-c)= (b+c)(a+c)(a+b) (*)
áp dụng BĐT cô-si: \(\left(b+c\right)\left(a+c\right)\left(a+b\right)\ge2\sqrt{bc}2\sqrt{ac}2\sqrt{ab}=8\sqrt{\left(abc\right)2}=8abc\) ( luôn đúng với mọi a,b,c ko âm )
b) áp dụng BĐT cô-si: \(c\left(a+b\right)\le\dfrac{\left(a+b+c\right)^2}{4}=\dfrac{1}{4}\)
Tương tự: \(a\left(b+c\right)\le\dfrac{1}{4};b\left(c+a\right)\le\dfrac{1}{4}\)
\(\Rightarrow abc\left(a+b\right)\left(b+c\right)\left(c+a\right)\le\dfrac{1}{4}\dfrac{1}{4}\dfrac{1}{4}=\dfrac{1}{64}\)

\(1,=x\left(x^2-2x+1\right)=x\left(x-1\right)^2\\ 2,=6\left(x^2+2xy+y^2\right)=6\left(x+y\right)^2\\ 3,=2y\left(y^2+4y+4\right)=2y\left(y+2\right)^2\\ 4,=2\left(x^2+2x+1-y^2\right)=2\left[\left(x+1\right)^2-y^2\right]\\ =2\left(x+y+1\right)\left(x-y+1\right)\\ 5,=16-\left(x-y\right)^2=\left(4-x+y\right)\left(4+x-y\right)\)

2) \(=6\left(x^2+2xy+y^2\right)=6\left(x+y\right)^2\)
3) \(=2y\left(y^2+4y+4\right)=2y\left(y+2\right)^2\)
4) \(=2\left[\left(x^2+2x+1\right)-y^2\right]=2\left[\left(x+1\right)^2-y^2\right]\)
\(=2\left(x+1-y\right)\left(x+1+y\right)\)
5) \(=16-\left(x^2-2xy+y^2\right)=16-\left(x-y\right)^2\)
\(=\left(4-x+y\right)\left(4+x-y\right)\)






 mn ơi giúp em, nhanh ạ, chỉ cần làm đến bài 2 thôi,bài 1 chỉ cần làm đến câu 17
mn ơi giúp em, nhanh ạ, chỉ cần làm đến bài 2 thôi,bài 1 chỉ cần làm đến câu 17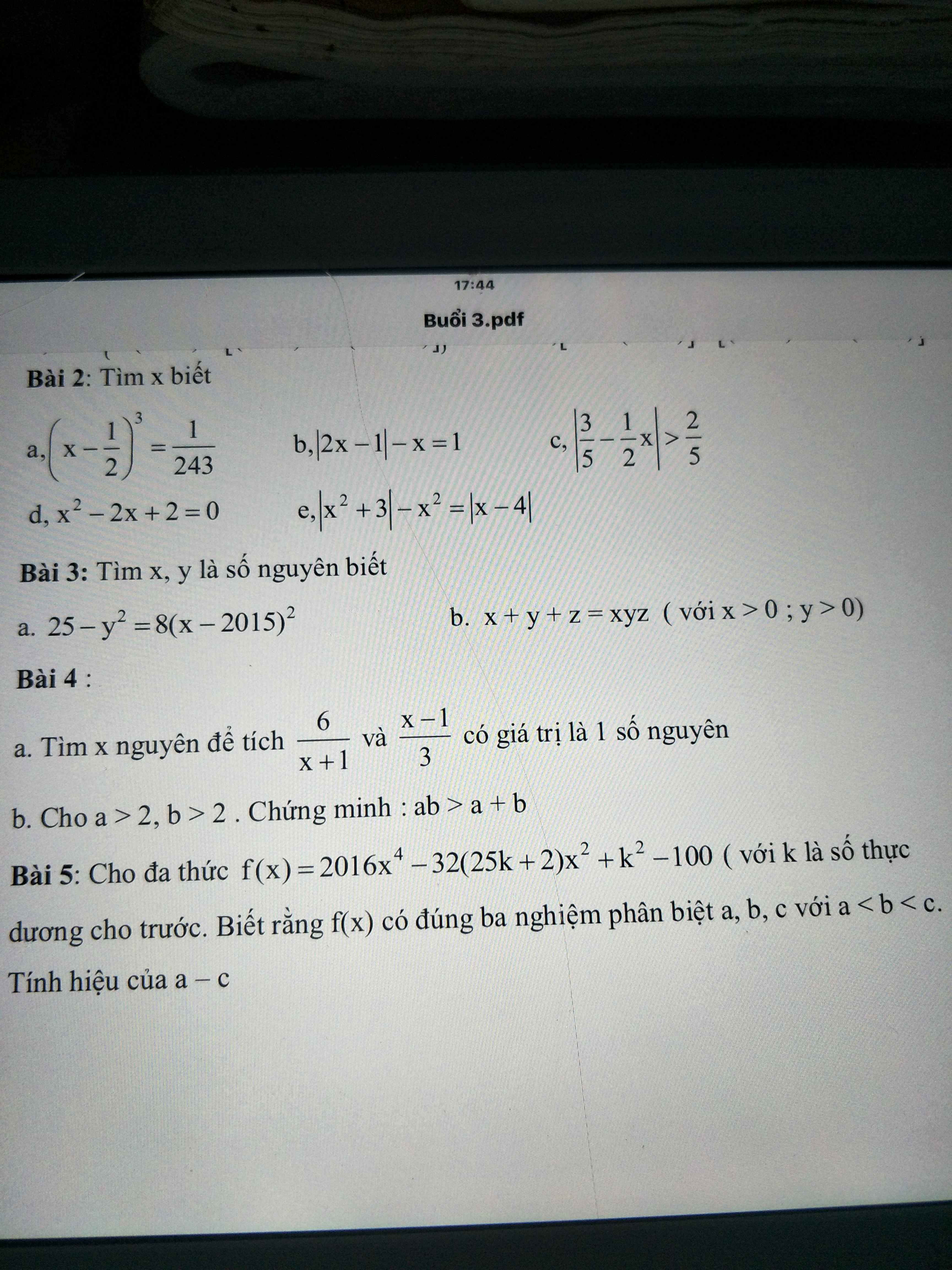

S = 1 x 2 x 3 x 4 x ....... x 300
S = ( 300 : 1 ) : ( 2 x 4 )
S = 37,5
Ta thấy 300 không chia được ra số có dư nên ta gạch 2 và 4