Cho hàm số y=f(x) có đạo hàm trên R và có đồ thị như hình vẽ
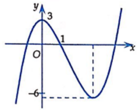
Đặt g x = 2 f x − 3 f x . Tìm số nghiệm của phương trình g’(x)=0
A. 5
B. 3
C. 2
D. 6
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
23 tháng 5 2017
Đúng(0)
Những câu hỏi liên quan
.
có 8 nghiệm phân biệt.
CM
20 tháng 1 2017
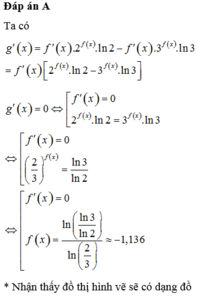
Đáp án B
Phương pháp: Lập bảng biến thiên của g(x) và đánh giá số giao điểm của đồ thị hàm số y = g(x) và trục hoành.
Cách giải: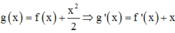 
Xét giao điểm của đồ thị hàm sốy = f’(x) và đường thẳng y = -x ta thấy, hai đồ thị cắt nhau tại ba điểm có hoành độ là: -2;2;4 tương ứng với 3 điểm cực trị của y = g(x).
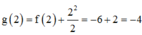
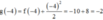
Bảng biến thiên:
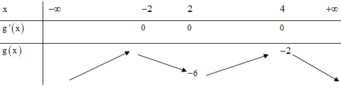
Dựa vào bảng biến thiên ta thấy 
=> phương trình g(x) = 0 không có nghiệm 
CM
29 tháng 8 2019
Đáp án B
Ta có
.
.
Hình bên dưới là đồ thị của hàm số 
và 
.
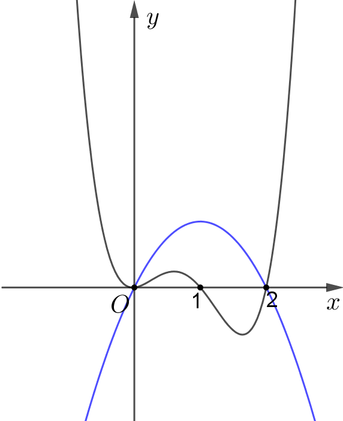
Dựa vào hình vẽ ta thấy đồ thị hàm số 
và 
cắt nhau tại 2 điểm phân biệt, đồng thời 
khi 
hoặc 
, 
khi 
.
Do đó 
đổi dấu qua 
, 
.
Vậy hàm số g(x) có hai điểm cực trị.
CM
8 tháng 12 2019
Đáp án A
Ta có g ' x = f ' x .2 f x . ln 2 − f ' x .3 f x . ln 3 = f ' x 2 f x . ln 2 − 3 f x . ln 3
g ' x = 0 ⇔ f ' x = 0 2 f x . ln 2 = 3 f x . ln 3 ⇔ f ' x = 0 2 3 f x = ln 3 ln 2 ⇔ f ' x = 0 f x = ln ln 3 ln 2 ln 2 3 ≈ − 1,136
* Nhận thấy đồ thị hình vẽ sẽ có dạng đồ thị hàm bậc ba, đồ thị có hai điểm cực trị nên phương trình f ' x = 0 có hai nghiệm phân biệt.
* Số nghiệm của phương trình f x = − 1,136 chính là số giao điểm của đồ thị hàm số f x với đường thẳng y = − 1,136 . Vậy phương trình f x = − 1,136 có 3 nghiệm phân biệt.
Vậy phương trình g ' x = 0 có 5 nghiệm phân biệt.
