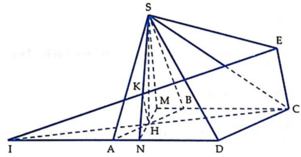
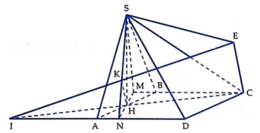
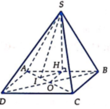
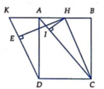
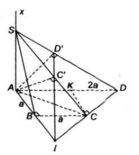
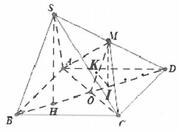
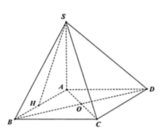
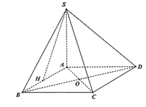
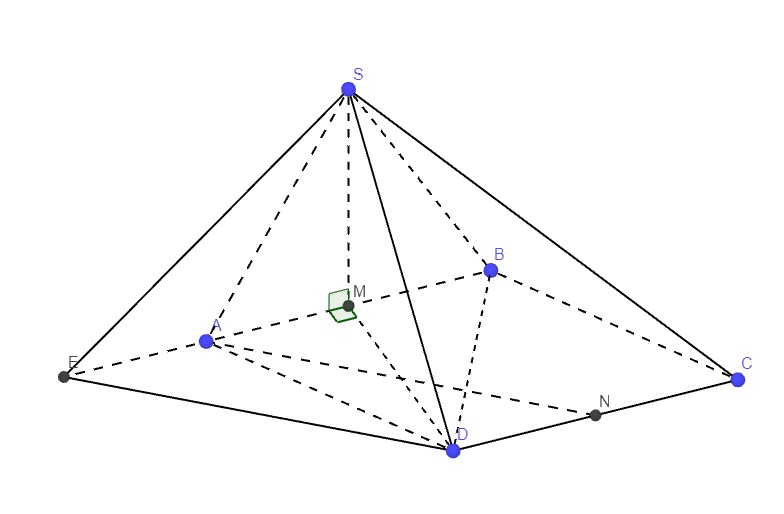
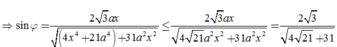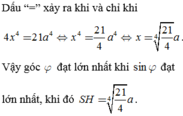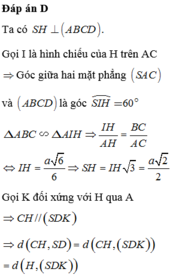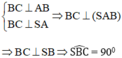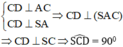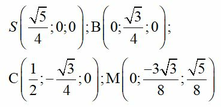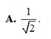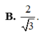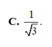Cho hình thoi ABCD có B A D ^ = 60 ° , A B = 2 a . Gọi H là trung điểm của AB. Trên đường thẳng d vuông góc với mặt phẳng (ABCD) tại H lấy điểm S thay đổi khác H. Trên tia đối của tia BC lấy điểm M sao cho B M = 1 4 B C . Tính theo a độ dài của SH để góc giữa SC và (SAD) có số đo lớn nhất
A. S H = 21 4 4 a .
B. S H = 21 4 4 a .
C. S H = 21 4 a .
D. S H = 21 4 a .