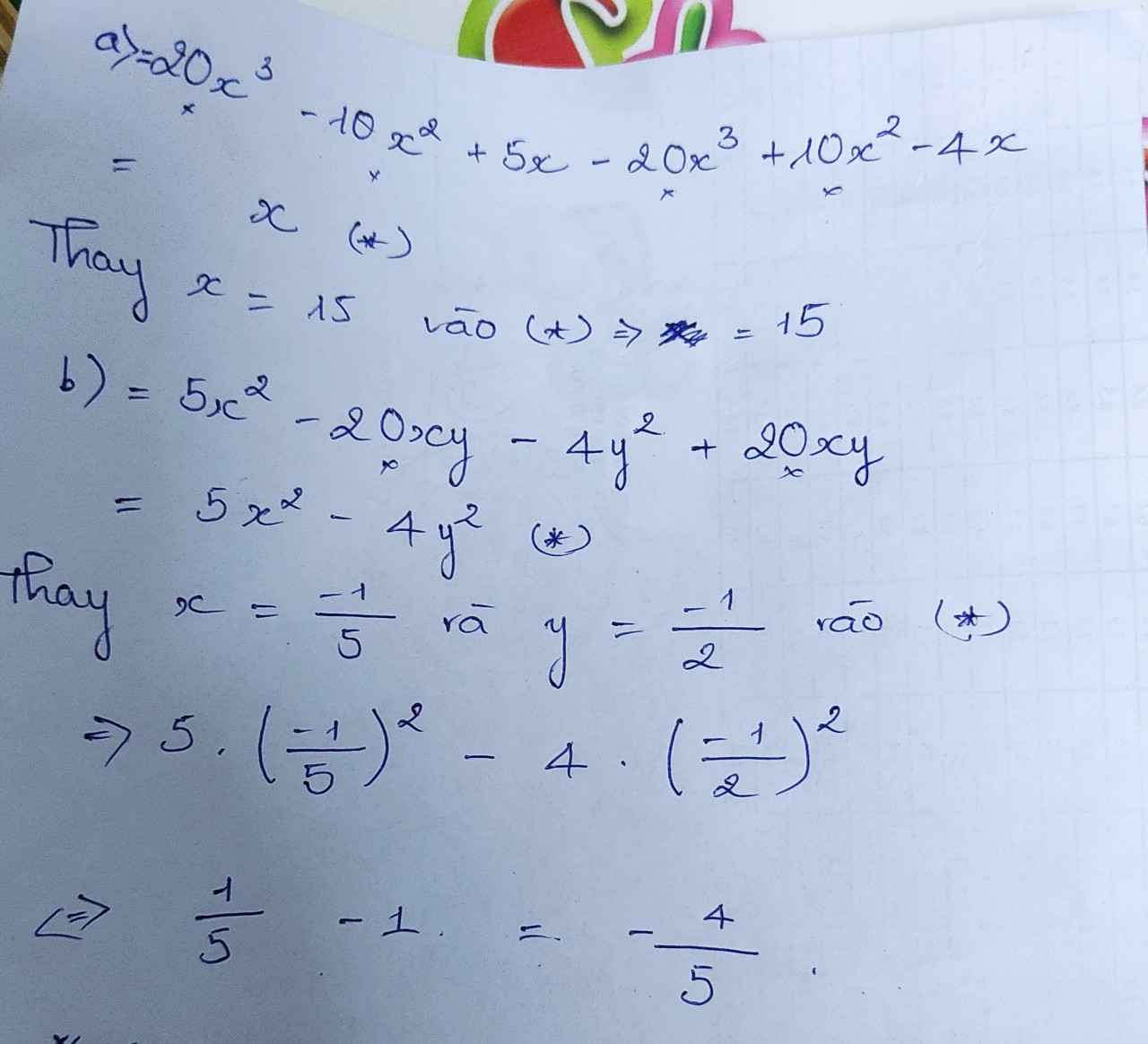Chứng minh: 3 + 2x - 4y + 6xy - 10x^2 +5y^2 > 0 với mọi giá trị x,y
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TT
20 tháng 12 2020
a/ \(A=20x^3-10x^2+5x-20x^3+10x^2+4x=9x\)
Thay x = 15 vào bt A ta có
A = 9 . 15 = 135
b/ \(B=5x^2-20xy-4y^2+2xy=5x^2-4y^2\)
Thay x = -1/5 ; y = - 1/2 vào bt B ta có
\(B=5.\dfrac{1}{25}-4.\dfrac{1}{4}=\dfrac{1}{5}-1=-\dfrac{4}{5}\)
c/ \(C=6x^2y^2-6xy^3-8x^3+8x^2y^2-5x^2y^2+5xy^3\)
\(=9x^2y^2-xy^3-8x^3\)
Thay x = 1/2 ; y = 2 vào bt C ta có
\(C=9.4.\dfrac{1}{4}-\dfrac{1}{2}.8-8.\dfrac{1}{8}=9-4-1=4\)
d/ \(D=6x^2+10x-3x-5+6x^2-3x+8x-2\)
\(=12x^2+12x-3\)
\(\left|x\right|=2\Rightarrow x=\pm2\)
Thay x = 2 vào bt D có
\(D=12.4+12.2-3=69\)
Thay x = - 2 vào bt D ta có
\(D=12.4-12.2-3=21\)
CE
0
AH
Akai Haruma
Giáo viên
27 tháng 8 2023
Bạn nên viết đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để mọi người hiểu đề của bạn hơn nhé.
12 tháng 10 2020
\(A=2x^2-20x+7=2\left(x^2-10x+25\right)-43=2\left(x-5\right)^2-43\ge-43\left(\forall x\right)\)
=> Chưa thể khẳng định A dương
\(B=9x^2-6xy+2y^2+1\)
\(B=\left(9x^2-6xy+y^2\right)+y^2+1\)
\(B=\left(3x-y\right)^2+y^2+1\ge1>0\left(\forall x\right)\)
=> đpcm
\(C=x^2-2x+y^2+4y+6\)
\(C=\left(x^2-2x+1\right)+\left(y^2+4y+4\right)+1\)
\(C=\left(x-1\right)^2+\left(y+2\right)^2+1\ge1>0\left(\forall x\right)\)
=> đpcm
\(D=x^2-2x+2=\left(x^2-2x+1\right)+1=\left(x-1\right)^2+1\ge1>0\left(\forall x\right)\)
=> đpcm
AH
Akai Haruma
Giáo viên
9 tháng 9 2021
Lời giải:
a.
$A=20x^3-10x^2+5x-(20x^3-10x^2-4x)$
$=9x=9.15=135$
b.
$B=(5x^2-20xy)-(4y^2-20xy)=5x^2-4y^2$
$=5(\frac{-1}{5})^2-4(\frac{-1}{2})^2=\frac{-4}{5}$
c.
$C=(6x^2y^2-6xy^3)-(8x^3-8x^2y^2)-(5x^2y^2-5xy^3)$
$=-8x^3+9x^2y^2-xy^3$
$=(-2x)^3+(3xy)^2-xy^3$
$=(-2.\frac{1}{2})^3+(3.\frac{1}{2}.2)^2-\frac{1}{2}.2^3$
$=(-1)^3+3^2-4=4$
MN
13 tháng 7 2021
\(a.\)
\(A=9x^2-6xy+2y^2+1\)
\(A=\left(3x\right)^2-2\cdot3x\cdot y+y^2+y^2+1\)
\(A=\left(3x-y\right)^2+\left(y^2+1\right)\ge0\)
\(b.\)
\(B=x^2-2x+y^2+4y+6\)
\(B=x^2-2x+1+y^2+4y+4+1\)
\(B=\left(x-1\right)^2+\left(y+2\right)^2+1\ge1\)
\(c.\)
\(C=x^2-2x+2\)
\(C=x^2-2x+1+1\)
\(C=\left(x-1\right)^2+1\ge1\)
13 tháng 7 2021
a) A=9x2-6xy+2y2+1
A=(3x)2-2.3x.y+y2+y2+1
A=(3x-y)2+(y2+1)≥0
Câu b, c tương tự câu a
NT
1
VT
3 tháng 10 2019
= (x2-x+1)(x2+3x+10)+10 = P
x2-x+1=(x-\(\frac{1}{2}\))2+\(\frac{3}{4}\)>0
x2+3x+10=(x+\(\frac{3}{2}\))2+\(\frac{31}{4}\)>0
vây P>0
HK
0