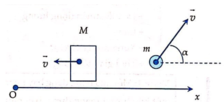
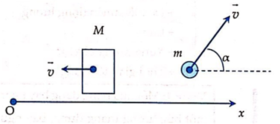
Một viên đạn được bắn ra với vận tốc ban đầu v 0 > 0 từ một nòng súng đặt ở gốc tọa độ O nghiêng một góc α với mặt đất (nòng súng nằm trong mặt phẳng thẳng đứng Oxy và tạo với trục hoành Ox góc α ). Biết quỹ đạo chuyển động của viên đạn là parabol γ α : y = - g 2 v 0 2 1 + tan 2 α x 2 + x tan α (với g là gia tốc trọng trường) và giả sử rằng quỹ đạo lấy luôn tiếp xúc với parabol an toàn T : y = - g 2 v 0 2 x 2 + v 0 2 2 g . Tìm tọa độ tiếp điểm khi α ∈ 0 ; π 2
A. M - v 0 2 g tan α ; v 0 2 2 g 1 - c o t 2 α
B. M v 0 2 g tan α ; v 0 2 2 g 1 - 1 tan 2 α
C. M v 0 2 tan α ; v 0 2 2 - g tan 2 α + 1 g
D. M v 0 2 tan α ; 1 2 v 0 2 g - g tan α

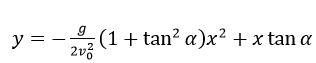
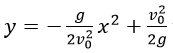
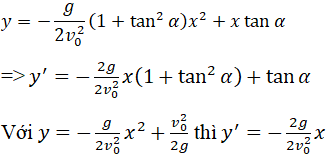
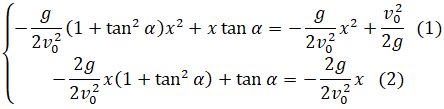
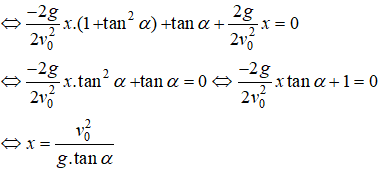
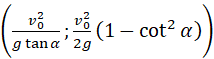


Xét γ α : y = - g 2 v 0 2 1 + tan 2 α x 2 + x tan α và T : y = - g 2 v 0 2 x 2 + v 0 2 2 g
γ α tiếp xúc T khi và chỉ khi hệ phương trình sau có nghiệm f x = g x 1 f ' x = g ' x 2
Ta có
2 ⇔ - g v 0 2 1 + tan 2 α x + tan α = - g v 0 2 x ⇔ - g v 0 2 tan 2 α x + tan α = 0 ⇔ x = v 0 2 g tan α
Đáp án B