Cho hình thang cân ABCD (AB // CD) có hai đường chéo cắt nhau tại I, hai đường thẳng AD và BC cắt nhau ở K. Chọn câu sai.
A. ΔKAB cân tại K.
B. ΔKCD cân tại K.
C. ΔICD đều.
D. KI là đường phân giác A K B ^ .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án cần chọn là: A
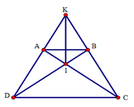
Xét tam giác ACD và tam giác BDC có:
+ AD = BC (do ABCD là hình thang cân)
+ AC = BD (do ABCD là hình thang cân)
+ CD là cạnh chung
Suy ra ΔACD = ΔBDC (c.c.c)
Suy ra A C D ^ = B D C ^ (cmt), suy ra tam giác ICD cân tại I. Do đó ID = IC (1)
Tam giác KCD có hai góc ở đáy bằng nhau nên tam giác KCD cân ở K.
Do đó KC = KD (2)
Từ (1) và (2) suy ra KI là đường trung trực của CD (*).
Xét tam giác ADB và tam giác BCA có:
+ AD = BC (cmt)
+ AB là cạnh chung
+ AC = BD
Suy ra ΔADB = ΔBCA (c.c.c)
Suy ra A B D ^ = B A C ^
Xét tam giác IAB có A B D ^ = B A C ^ nên tam giác IAB cân tại I.
Do đó IA = IB (3)
Ta có KA = KD – AD; KB = KC – BC
Mà KD = KC, AD = BC, do đó KA = KB (4)
Từ (3) và (4) suy ra KI là đường trung trực của AB. (**)
Từ (*) và (**) suy ra KI là đường trung trực của hai đáy (đpcm)

1.
+) Tứ giác ABCD kà hình thang cân => góc ADC = BCD và AD = BC
=> tam giác ODC cân tại O => OD = OC
mà AD = BC => OA = OB
+) tam giác ODB và OCA có: OD = OC; góc DOC chung ; OB = OA
=> Tam giác ODB = OCA (c - g - c)
=> góc ODB = OCA mà góc ODC = OCD => góc ODC - ODB = OCD - OCA
=> góc EDC = ECD => tam giác EDC cân tại E => ED = EC (2)
Từ (1)(2) => OE là đường trung trực của CD
=> OE vuông góc CD mà CD // AB => OE vuông góc với AB
Tam giác OAB cân tại O có OE là đường cao nên đồng thời là đường trung trực
vậy OE là đường trung trực của AB

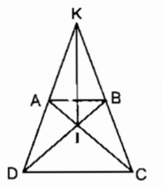
∆ ACD = ∆ BDC (c.c.c)
Suy ra 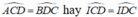
⇒ Tam giác ICD cân tại I.
do đó ID = IC (1)
Tam giác KCD có hai góc ở đáy bằng nhau ∠ C = ∠ D nên tam giác KCD cân tại K
⇒ KD = KC (2)
Từ (1) và (2) suy ra KI là đường trung trực của CD.
Chứng minh tương tự có IA = IB, KA = KB
Suy ra KI là đường trung trực của AB

Rút gọn các biểu thức sau :
a,3√5−√2 +4√6+√2
b (√20−√45+√5).√5
c,(5√15 +12 √20−54 √45 +√5):2√5
d 2√3(2√6−√3+1)
e √2+√3×√2−√3
g 5√7−7√5+2√70√35
h (√23 +√32 )×√6
i (1+√2+√3)×(1+√2−√3)
k 1√5+√3 −1√5−√3
l 12+√3 +√2√6 −23+√3
m
giả sử DC>AB, ta chứng minh tam giác KDC cân tại Kthì K thuộc đường trung trực 2 đáy, còn chứng minh 2 tam giác = nhau đẻ => 2 goc= nhau , rồi có tam giác IDC cân tại I và I thuộc đường rung trực của DC
=> đpcm

Bài 2:
Ta có: \(\widehat{ACD}=\widehat{ACB}+\widehat{DCB}\)(tia CB nằm giữa hai tia CA và CD)
\(\Leftrightarrow\widehat{ACD}=45^0+45^0=90^0\)
Xét tứ giác ACDB có
CD//AB(cùng vuông góc với AC)
nên ACDB là hình thang có hai đáy là CD và AB(Định nghĩa hình thang)
Hình thang ACDB(CD//AB) có \(\widehat{CAB}=90^0\)(gt)
nên ACDB là hình thang vuông(Định nghĩa hình thang vuông)
Đáp án cần chọn là: C
Xét tam giác ACD và tam giác BDC có:
+ AD = BC (do ABCD là hình thang cân)
+ AC = BD (do ABCD là hình thang cân)
+ CD là cạnh chung
Suy ra ΔACD = ΔBDC (c.c.c)
Suy ra A C D ^ = B D C ^ (hai góc tương ứng), suy ra tam giác ICD cân tại I.
Nên C sai vì ta chưa đủ điều kiện để IC = CD
Tam giác KCD có hai góc ở đáy bằng nhau nên tam giác KCD cân ở K nên B đúng.
Xét tam giác KDI và tam giác KCI có:
+ KD = KC (do ΔKCD cân tại K))
+ KI là cạnh chung
+ IC = ID
Suy ra ΔKDI = ΔKCI (c.c.c)
Suy ra K D I ^ = C K I ^ , do đó KI là phân giác A K B ^ nên D đúng.
Ta có AB // CD (do ABCD là hình thang) nên K A B ^ = K C D ^ ; K B A ^ = K C D ^ (các cặp góc đồng vị bằng nhau)
Mà K D C ^ = K C D ^ (tính chất hình thang cân) nên K A B ^ = K C D ^ (tính chất hình thang cân) nên hay ΔKAB cân tại K. Do đó A đúng