Giả sử x, y thuộc tập hợp số thực để 1/x - 1/2y = 1/2x+y. Tìm giá trị của x^2/y^2 + y^2/x^2.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(1,\\ a,\dfrac{x^2}{x+1}+\dfrac{x}{x+1}=\dfrac{x^2+x}{x+1}=\dfrac{x\left(x+1\right)}{x+1}=x\)
\(b,\left(\dfrac{2xy}{x^2-y^2}+\dfrac{x-y}{2x+2y}\right):\dfrac{x+y}{2x}=\left(\dfrac{4xy}{2\left(x-y\right)\left(x+y\right)}+\dfrac{\left(x-y\right)^2}{2\left(x-y\right)\left(x+y\right)}\right).\dfrac{2x}{x+y}=\dfrac{4xy+x^2-2xy+y^2}{2\left(x-y\right)\left(x+y\right)}.\dfrac{2x}{x+y}=\dfrac{2x\left(x^2+2xy+y^2\right)}{2\left(x-y\right)\left(x+y\right)^2}=\dfrac{2x\left(x+y\right)^2}{2\left(x-y\right)\left(x+y\right)^2}=\dfrac{x}{x-y}\)

Do \(1\le x\le2\Rightarrow\left(x-1\right)\left(x-2\right)\le0\)
\(\Leftrightarrow x^2+2\le3x\)
Hoàn toàn tương tự ta có \(y^2+2\le3y\)
Do đó: \(P\ge\dfrac{x+2y}{3x+3y+3}+\dfrac{2x+y}{3x+3y+3}+\dfrac{1}{4\left(x+y-1\right)}\)
\(P\ge\dfrac{x+y}{x+y+1}+\dfrac{1}{4\left(x+y-1\right)}\)
Đặt \(a=x+y-1\Rightarrow1\le a\le3\)
\(\Rightarrow P\ge f\left(a\right)=\dfrac{a+1}{a+2}+\dfrac{1}{4a}\)
\(f'\left(a\right)=\dfrac{3a^2-4a-4}{4a^2\left(a+2\right)^2}=\dfrac{\left(a-2\right)\left(3a+2\right)}{4a^2\left(a+2\right)^2}=0\Rightarrow a=2\)
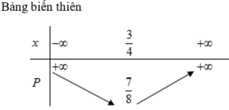
\(f\left(1\right)=\dfrac{11}{12}\) ; \(f\left(2\right)=\dfrac{7}{8}\) ; \(f\left(3\right)=\dfrac{53}{60}\)
\(\Rightarrow f\left(a\right)\ge\dfrac{7}{8}\Rightarrow P_{min}=\dfrac{7}{8}\) khi \(\left(x;y\right)=\left(1;2\right);\left(2;1\right)\)

a: \(y=-x^2+2x+3\)
y>0
=>\(-x^2+2x+3>0\)
=>\(x^2-2x-3< 0\)
=>(x-3)(x+1)<0
TH1: \(\left\{{}\begin{matrix}x-3>0\\x+1< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>3\\x< -1\end{matrix}\right.\)
=>\(x\in\varnothing\)
TH2: \(\left\{{}\begin{matrix}x-3< 0\\x+1>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x< 3\\x>-1\end{matrix}\right.\)
=>-1<x<3
\(y=\dfrac{1}{2}x^2+x+4\)
y>0
=>\(\dfrac{1}{2}x^2+x+4>0\)
\(\Leftrightarrow x^2+2x+8>0\)
=>\(x^2+2x+1+7>0\)
=>\(\left(x+1\right)^2+7>0\)(luôn đúng)
b: \(y=-x^2+2x+3< 0\)
=>\(x^2-2x-3>0\)
=>(x-3)(x+1)>0
TH1: \(\left\{{}\begin{matrix}x-3>0\\x+1>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>3\\x>-1\end{matrix}\right.\)
=>x>3
TH2: \(\left\{{}\begin{matrix}x-3< 0\\x+1< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x< 3\\x< -1\end{matrix}\right.\)
=>x<-1
\(y=\dfrac{1}{2}x^2+x+4\)
\(y< 0\)
=>\(\dfrac{1}{2}x^2+x+4< 0\)
=>\(x^2+2x+8< 0\)
=>(x+1)2+7<0(vô lý)

Ta sẽ chứng minh \(P_{min}=1\)
TH1: \(xyz=0\)
\(\Rightarrow x^2y^2z^2=0\Rightarrow x^4+y^4+z^4=1\)
\(P=x^2+y^2+z^2\ge\sqrt{x^4+y^4+z^4}=1\)
TH2: \(xyz\ne0\) , từ điều kiện, tồn tại 1 tam giác nhọn ABC sao cho \(\left\{{}\begin{matrix}x^2=cosA\\y^2=cosB\\z^2=cosC\end{matrix}\right.\)
\(P=cosA+cosB+cosC-\sqrt{2cosA.cosB.cosC}\)
Ta sẽ chứng minh \(cosA+cosB+cosC-\sqrt{2cosA.cosB.cosC}\ge1\)
\(\Leftrightarrow4sin\dfrac{A}{2}sin\dfrac{B}{2}sin\dfrac{C}{2}\ge\sqrt{2cosA.cosB.cosC}\)
\(\Leftrightarrow8sin^2\dfrac{A}{2}sin^2\dfrac{B}{2}sin^2\dfrac{C}{2}\ge cosA.cosB.cosC\)
\(\Leftrightarrow\dfrac{8sin^2\dfrac{A}{2}sin^2\dfrac{B}{2}sin^2\dfrac{C}{2}}{8sin\dfrac{A}{2}sin\dfrac{B}{2}sin\dfrac{C}{2}cos\dfrac{A}{2}cos\dfrac{B}{2}cos\dfrac{C}{2}}\ge cotA.cotB.cotC\)
\(\Leftrightarrow tan\dfrac{A}{2}tan\dfrac{B}{2}tan\dfrac{C}{2}\ge cotA.cotB.cotC\)
\(\Leftrightarrow tanA.tanB.tanC\ge cot\dfrac{A}{2}cot\dfrac{B}{2}cot\dfrac{C}{2}\)
\(\Leftrightarrow tanA+tanB+tanC\ge cot\dfrac{A}{2}+cot\dfrac{B}{2}+cot\dfrac{C}{2}\)
Ta có:
\(tanA+tanB=\dfrac{sin\left(A+B\right)}{cosA.cosB}=\dfrac{2sinC}{cos\left(A-B\right)-cosC}\ge\dfrac{2sinC}{1-cosC}=\dfrac{2sin\dfrac{C}{2}cos\dfrac{C}{2}}{2sin^2\dfrac{C}{2}}=cot\dfrac{C}{2}\)
Tương tự: \(tanA+tanC\ge cot\dfrac{B}{2}\) ; \(tanB+tanC\ge cot\dfrac{A}{2}\)
Cộng vế với vế ta có đpcm
Vậy \(P_{min}=1\) khi \(\left(x^2;y^2;z^2\right)=\left(1;0;0\right)\) và các hoán vị hoặc \(\left(x^2;y^2;z^2\right)=\left(\dfrac{1}{2};\dfrac{1}{2};\dfrac{1}{2}\right)\)
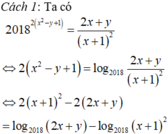
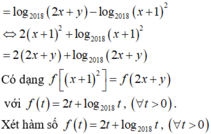

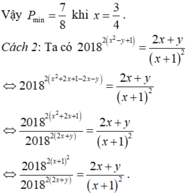


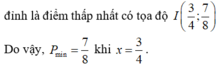

\(\frac{1}{x}-\frac{1}{2y}=\frac{1}{2x+y}\)
=> \(\frac{2y-x}{2xy}=\frac{1}{2x+y}\)
=> (2y - x)(2x + y) = 2xy
=> 4xy + 2y2 - 2x2 - xy = 2xy
=> 2(y2- x2) = -xy
=> [2(y2 - x2)]2 = (-xy)2
=> 4(y2 - x2)2 = (xy)2
=> 4(y4 - 2(xy)2 + x4) = (xy)2
=> 4y4 - 8(xy)2 + 4x4 = (xy)2
=> 4(y4 + x4) = 9(xy)2
=> y4 + x4 = \(\frac{9}{4}\left(xy\right)^2\)
Khi đó \(\frac{x^2}{y^2}+\frac{y^2}{x^2}=\frac{x^4+y^4}{\left(xy\right)^2}=\frac{\frac{9}{4}\left(xy\right)^2}{\left(xy\right)^2}=\frac{9}{4}\)