Giải phương...
Đọc tiếp
Giải phương trình
a)
b)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
Y
24 tháng 6 2023
\(a,4+x^2+4x=0\)
\(\Leftrightarrow x^2+4x+4=0\)
\(\Leftrightarrow\left(x+2\right)^2=0\)
\(\Leftrightarrow x+2=0\)
\(\Leftrightarrow x=-2\)
Vậy \(S=\left\{-2\right\}\)
\(b,-6x+9+x^2=0\)
\(\Leftrightarrow x^2-6x+9=0\)
\(\Leftrightarrow\left(x-3\right)^2=0\)
\(\Leftrightarrow x-3=0\)
\(\Leftrightarrow x=3\)
Vậy \(S=\left\{3\right\}\)
24 tháng 2 2022
\(a)\left(x-2\right)\left(x^2+2x-3\right)\ge0.\)
Đặt \(f\left(x\right)=\left(x-2\right)\left(x^2+2x-3\right).\)
Ta có: \(x-2=0.\Leftrightarrow x=2.\\ x^2+2x-3=0.\Leftrightarrow\left[{}\begin{matrix}x=1.\\x=-3.\end{matrix}\right.\)
Bảng xét dấu:
x \(-\infty\) -3 1 2 \(+\infty\)
\(x-2\) - | - | - 0 +
\(x^2+2x-3\) + 0 - 0 + | +
\(f\left(x\right)\) - 0 + 0 - 0 +
Vậy \(f\left(x\right)\ge0.\Leftrightarrow x\in\left[-3;1\right]\cup[2;+\infty).\)
\(b)\dfrac{x^2-9}{-x+5}< 0.\)
Đặt \(g\left(x\right)=\dfrac{x^2-9}{-x+5}.\)
Ta có: \(x^2-9=0.\Leftrightarrow\left[{}\begin{matrix}x=3.\\x=-3.\end{matrix}\right.\)
\(-x+5=0.\Leftrightarrow x=5.\)
Bảng xét dấu:
x \(-\infty\) -3 3 5 \(+\infty\)
\(x^2-9\) + 0 - 0 + | +
\(-x+5\) + | + | + 0 -
\(g\left(x\right)\) + 0 - 0 + || -
Vậy \(g\left(x\right)< 0.\Leftrightarrow x\in\left(-3;3\right)\cup\left(5;+\infty\right).\)
PN
15 tháng 5 2021
\(|x-6|=-5x+9\)
Xét \(x\ge6\)thì \(pt< =>x-6=-5x+9\)
\(< =>x-6+5x-9=0\)
\(< =>6x-15=0\)
\(< =>x=\frac{15}{6}\)(ktm)
Xét \(x< 6\)thì \(pt< =>x-6=5x-9\)
\(< =>4x-9+6=0\)
\(< =>4x-3=0< =>x=\frac{3}{4}\)(tm)
Vậy ...
NH
3
A
17 tháng 7 2019
ý bạn là như thế này đúng không ạ:
a/ \(x^2-6x+5=0\)
\(x^2-5x-x+5=0\)
\(x\left(x-5\right)-\left(x-5\right)=0\)
\(\left(x-5\right)\left(x-1\right)=0\)
\(\orbr{\begin{cases}x-5=0\rightarrow x=5\\x-1=0\rightarrow x=1\end{cases}}\)
b/\(2x^2+7x+9=0\)
?!
c/ \(4x^2-7x+3=0\)
\(4x^2-4x-3x+3=0\)
\(4x\left(x-1\right)-3\left(x-1\right)=0\)
\(\left(x-1\right)\left(4x-3\right)=0\)
\(\orbr{\begin{cases}x-1=0\Rightarrow x=1\\4x-3=0\Rightarrow x=\frac{3}{4}\end{cases}}\)
d/ \(2\left(x+5\right)=2x+10\)
-,- mik ko rõ đề ạ, sai thì ibox ạ.Cảm ơn
RH
18 tháng 2 2022
\(a)x^2-9x+20=0 \\<=>(x-4)(x-5)=0 \\<=>x=4\ hoặc\ x=5 \\b)x^2-3x-18=0 \\<=>(x+3)(x-6)=0 \\<=>x=-3\ hoặc\ x=6 \\c)2x^2-9x+9=0 \\<=>(x-3)(2x-3)=0 \\<=>x=3\ hoặc\ x=\dfrac{3}{2}\)
18 tháng 2 2022
d: \(\Leftrightarrow3x^2-6x-2x+4=0\)
=>(x-2)(3x-2)=0
=>x=2 hoặc x=2/3
e: \(\Leftrightarrow3x\left(x^2-2x-3\right)=0\)
=>x(x-3)(x+1)=0
hay \(x\in\left\{0;3;-1\right\}\)
f: \(\Leftrightarrow x^2-5x-2+x=0\)
\(\Leftrightarrow x^2-4x-2=0\)
\(\Leftrightarrow\left(x-2\right)^2=6\)
hay \(x\in\left\{\sqrt{6}+2;-\sqrt{6}+2\right\}\)
NH
4
16 tháng 1 2021
\(a,\left(2x-3\right)^2=\left(x+1\right)^2\\ \Leftrightarrow\left(2x-3\right)^2-\left(x+1\right)^2=0\\ \Leftrightarrow\left(2x-3+x+1\right)\left(2x-3-x-1\right)=0\\ \Leftrightarrow\left(3x-2\right)\left(x-4\right)\\ \Leftrightarrow\left[{}\begin{matrix}3x-2=0\\x-4=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}3x=2\\x=4\end{matrix}\right. \\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{2}{3}\\x=4\end{matrix}\right.\)
Vậy \(x\in\left\{\dfrac{2}{3};4\right\}\)
16 tháng 1 2021
\(b,x^2-6x+9=9\left(x-1\right)^2\\ \Leftrightarrow\left(x-3\right)^2=9\left(x-1\right)^2\\ \Leftrightarrow\left(x-3\right)^2-9\left(x-1\right)^2=0\\ \Leftrightarrow\left(x-3\right)^2-3^2\left(x-1\right)^2=0\\ \Leftrightarrow\left(x-3\right)^2-\left[3\left(x-1\right)\right]^2=0\\ \Leftrightarrow\left(x-3\right)^2-\left(3x-3\right)^2=0\\ \Leftrightarrow\left(x-3+3x-3\right)\left(x-3-3x+3\right)=0\\ \Leftrightarrow-2x\left(4x-6\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}-2x=0\\4x-6=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\4x=6\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{3}{2}\end{matrix}\right.\)
Vậy \(x\in\left\{0;\dfrac{3}{2}\right\}\)
CM
1 tháng 12 2019
Đáp án B.
Ta có:
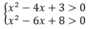
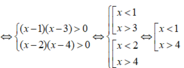
Vậy tập nghiệm của bất phương trình là: ( - ∞ ;1) ∪ (4; + ∞ )
CM
12 tháng 11 2017
Chọn B.
Ta có:
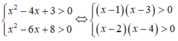
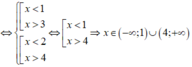
Vậy tập nghiệm của bất phương trình là S = ( - ∞ ;1) ∪ (4; + ∞ ).
CM
3 tháng 10 2019
Đáp án: A
Ta có bảng xét dấu:
Dựa vào bảng xét dấu ta thấy tập nghiệm của bất phương trình là: (- ∞ ;1) ∪ (4;+ ∞ )
\(a)\)√x2−9+√x2−6x+9=0x2−9+x2−6x+9=0
⇒√(x−3)(x+3)+√(x−3)2=0⇒(x−3)(x+3)+(x−3)2=0
⇒√(x−3)(x+3)+x−3=0⇒(x−3)(x+3)+x−3=0
Đặt x−3=tx−3=t pt thành
√t(t−6)−t=0t(t−6)−t=0
⇔t2−6t=t2⇔t2−6t=t2
⇔t=0⇔t=0⇒x−3=0⇔x=3
\(b)\)√x2−4−x2+4=0x2−4−x2+4=0
⇔√x2−4=x2−4⇔x2−4=x2−4
Đặt √x2−4=tx2−4=t pt thành
t=t2⇒t(1−t)=0t=t2⇒t(1−t)=0
⇒[t=1t=0⇒[t=1t=0.
Với t=0⇒√x2−4=0⇒x=±2t=0⇒x2−4=0⇒x=±2
Với t=1⇒√x2−4=1t=1⇒x2−4=1⇒x=±√5