trong hệ trục tọa độ oxy cho đường thẳng d:y=2x-2 và điểm I(3;-2).Hãy tính khoảng cách:
a)Từ O đến d
b)từ I đến d
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

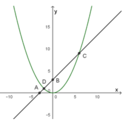
1) Xác định được ít nhất hai điểm phân biệt thuộc đường thẳng d. Chẳng hạn: A ( − 3 ; 0 ) ; B ( 0 ; 3 ) .
Xác định được đỉnh và ít nhất hai điểm thuộc (P) . Chẳng hạn : O ( 0 ; 0 ) ; C ( 6 ; 9 ) ; E ( − 6 ; 9 ) .
Đồ thị
2) Phương trình hoành độ giao điểm: 1 4 x 2 = x + 3 ⇔ 1 4 x 2 − x − 3 = 0 ⇔ x = − 2 hoặc x= 6
Tọa độ giao điểm là D ( − 2 ; 1 ) v à C ( 6 ; 9 ) .

Phương trình hoành độ giao điểm là:
\(x^2-x+3=2x+3\)
=>x(x-3)=0
=>x=0 hoặc x=3
=>y=3 hoặc y=9

N(a, 2a-2); M(b, b-4). giải hpt sau
\(\begin{cases}\\\overrightarrow{ON}=k.\overrightarrow{OM}\end{cases}OM^2.ON^2=64\)
dùng pp thế đc 1 phương trình bậc 4 theo 2 hoặc b

1,\(\overrightarrow{n}\)d=(2;-4)
d: 2(x+1)-4(y-1)=0⇔2x-4y+6=0
2) AM nhỏ nhất khi AM vuông góc với D
⇒\(\overrightarrow{n}\)AM=(4;2)
AM: 4(x+1)+2(y-1)=0⇔4x+2y+2=0
M=AM\(\cap\)D⇒Tọa độ điểm M là nghiệm của hệ:2x-4y=-1
4x+2y=-2
⇒M(-1/2;0)

1. Gọi đường thẳng cần tìm là (d): y = ax + b.
Giao điểm của (d) và Oy là A (0;2) => b = 2 (1).
Giao điểm của (d) và Ox là B (-2;0) => 2a + b = 0 (2)
Từ (1) và (2) ta có a = -1, b = 2. Vậy (d): y = -x + 2.
2. \(\left\{{}\begin{matrix}mx-2x+y=3\\3x-2y=m\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2mx-4x+2y=6\\3x-2y=m\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2mx-x=m+6\\3x-2y=m\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\left(2m-1\right)=m+6\\3x-2y=m\end{matrix}\right.\)
Để hệ có nghiệm duy nhất thì pt \(x\left(2m-1\right)=m+6\) có nghiệm duy nhất. Khi đó \(2m-1\ne0\Leftrightarrow m\ne\dfrac{1}{2}.\)
3.
2x + 3y + 5 = 0 ⇔ \(y=\dfrac{-2}{3}x-\dfrac{5}{3}\)
Để hai đường thẳng trùng nhau thì \(a=\dfrac{-2}{3};b=\dfrac{-5}{3}\).
4.
Bán kính đường tròn ngoại tiếp hình vuông là \(\dfrac{\sqrt{2}}{\sqrt{2}}=1\left(cm\right)\).
Độ dài đường tròn ngoại tiếp hình vuông là: 2π (cm).