Cho tam giác ABC,biết rằng số đo các góc A,B,C tỉ lệ với 2,3,4.Tính số đo của góc A
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi số góc `A,B,C` lần lượt là `a,b,c`
Theo đề ra ta có : `a/2=b/3=c/4` và `a+b+c=180`
ADTC dãy tỉ số bằng nhau ta có :
`a/2=b/3=c/4 =(a+b+c)/(2+3+4)=180/9= 20`
`=> a/2=20=>a=20.2=40`
Vậy số đo góc A là `40`

Tổng số đo các góc của hình tam giác luôn bằng 360 độ
Số đo của góc A là:360:(3+5+7)x3=72 độ
Số đo của góc B là:72:3x5=120 độ
Số đo của góc C là:360-120-72=168 độ

1:
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}=\dfrac{a+b+c}{2+3+4}=\dfrac{180}{9}=20\)
Do đó: a=40; b=60; c=80
Xét ΔABC có \(\widehat{A}< \widehat{B}< \widehat{C}\)
nen BC<AC<AB
2: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{b}{\dfrac{1}{3}}=\dfrac{c}{\dfrac{1}{4}}=\dfrac{b+c}{\dfrac{1}{3}+\dfrac{1}{4}}=\dfrac{70}{\dfrac{7}{12}}=120\)
Do đó: b=40; c=30
Xét ΔABC có \(\widehat{A}>\widehat{B}>\widehat{C}\)
nên BC>AC>AB

\(\dfrac{\widehat{A}}{3}=\dfrac{\widehat{B}}{5}=\dfrac{\widehat{C}}{7}=\dfrac{\widehat{A}+\widehat{B}+\widehat{C}}{3+5+7}=\dfrac{180^0}{15}=12^0\\ \Rightarrow\left\{{}\begin{matrix}\widehat{A}=36^0\\\widehat{B}=60^0\\\widehat{C}=84^0\end{matrix}\right.\)

Gọi a, b, c (độ) lần lượt là số đo 3 góc A, B, C. (0 < a; b; c < 180º).
Theo định lí tổng ba góc của tam giác ta có:
a + b + c = 180.
Vì số đo 3 góc tỉ lệ với 3; 5; 7 nên ta có:
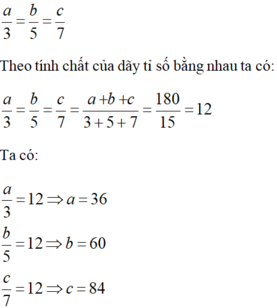
Vậy số đo ba góc của tam giác ABC là: 36o; 60o; 84o

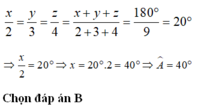
Theo bài ta có: \(\frac{\widehat{A}}{2}=\frac{\widehat{B}}{3}=\frac{\widehat{C}}{4}\)
mà \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)( tổng 3 góc trong tam giác )
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{\widehat{A}}{2}=\frac{\widehat{B}}{3}=\frac{\widehat{C}}{4}=\frac{\widehat{A}+\widehat{B}+\widehat{C}}{2+3+4}=\frac{180^o}{9}=20^o\)
\(\Rightarrow\widehat{A}=2.20^o=40^o\); \(\widehat{B}=3.20^o=60^o\); \(\widehat{C}=4.20^o=80^o\)
Vậy \(\widehat{A}=40^o\); \(\widehat{B}=60^o\); \(\widehat{C}=80^o\)
Gọi số đo của ba góc A,B,C là a,b,c ( 0 < a,b,c < 180o )
Vì số đo của các góc A,B,C tỉ lệ với 2,3,4
\(\Rightarrow\frac{a}{2}=\frac{b}{3}=\frac{c}{4}\)
mà a + b + c = 180 ( tổng 3 góc trong tam giác )
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{a}{2}=\frac{b}{3}=\frac{c}{4}\)\(=\frac{a+b+c}{2+3+4}\)\(=\frac{180}{9}=20\)
Suy ra : \(a=20\times2=40\)
Vậy \(\widehat{A}=40^o\)