Có bao nhiêu số tự nhiên n thỏa mãn n^2+3n +6 là bội của n +3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NN
0
NC
1
BH
1
11 tháng 12 2021
\(\Rightarrow n+2+4⋮n+2\\ \Rightarrow n+2\inƯ\left(4\right)=\left\{1;2;4\right\}\\ \Rightarrow n\in\left\{0;2\right\}\left(n\in N\right)\)
Vậy có 2 số
PT
1
CM
19 tháng 11 2018
Đáp án A
Ký hiệu B là biến cố lấy được số tự nhiên A thỏa mãn yêu cầu bài toán.
Ta có 3N = A <=> N = log3A
Để N là số tự nhiên thì A = 3m (m ∈ N)
Những số A dạng có 4 chữ số gồm 37 = 2187 và 38 = 6561
TX
1
LH
27 tháng 5 2018
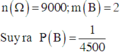
2019 = 3*673
n^3 +2019 chia hết cho 6 => n^3 + 2019 chia hết cho 3
Mà 2019 chia hết cho 3 nên n^3 chia hết cho 3 => n chia hết cho 3.
n^3 + 2019 chia hết cho 6 => n^3 + 2019 chia hết cho 2
Mà 2019 là số lẻ nên n^3 phải lẻ => n lẻ
Vậy n là số lẻ chia hết cho 3 thì n^3 + 2019 chia hết cho 6 (3,9,...,2019)
Số tự nhiên n thỏa mãn: (2019-3)/6 + 1 = 337
ta có : n^2 + 3n + 6 = n (n + 3) + 6
vì n(n + 3) : n + 3 nên 6 : n + 3
Ư(6) = 6 ; 3 ; 2 ; 1
vì n là STN nên n = 6 - 3 ; 3 - 3 = 3 ; 0
kết luận có 2 STN n