Tìm các số a,b biết:
a) BCNN(a,b) =120 và a nhân b =1200
b) ƯCLN(a,b)= 18 và 3a=7b
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AT
2
6 tháng 12 2016
Ta có:\(3a=7b\Leftrightarrow\frac{a}{7}=\frac{b}{3}\)
Đặt \(\frac{a}{7}=\frac{b}{3}=k\Rightarrow\hept{\begin{cases}a=7k\\b=3k\end{cases}}\) mà UCLN(a,b)=18
\(\Rightarrow UCLN\left(3k,7k\right)=18\)
mà UCLN(3,7)=1 nên k=18
\(\Rightarrow\hept{\begin{cases}a=7.18=126\\b=3.18=54\end{cases}}\)
PT
1
CM
24 tháng 11 2018
Vì (a,b) = 6 nên a = 6x, b = 6y, với (x,y)=1
Suy ra a.b=6x.6y = 36xy.
Lại có a.b = [a,b].(a,b) = 120.6 = 720
Suy ra 36xy = 720 => xy = 20
Giả sử x < y, và (x,y)=1 ta có các trường hợp sau:
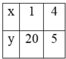
Từ đó suy ra a,b có các trường hợp sau:
PT
1
11 tháng 12 2019
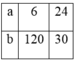
a. Bài làm :
Ta có : \(\hept{\begin{cases}ab=2400\\BCNN\left(a,b\right)=120\end{cases}}\)
\(\Rightarrow\)ƯCLN(a,b)=ab:BCNN(a,b)=2400:120=20
Vì ƯCLN(a,b)=20 nên ta có : \(\hept{\begin{cases}a=20m\\b=20n\\ƯCLN\left(m,n\right)=1\end{cases}}\)
Mà ab=2400
\(\Rightarrow\)20m.20n=2400
\(\Rightarrow\)400m.n=2400
\(\Rightarrow\)mn=6
Vì ƯCLN(m,n)=1 nên ta có bảng sau :
m 1 6 2 3
n 6 1 3 2
a 20 120 40 60
b 120 20 60 40
Vậy (a;b)\(\in\){(20;120);(120;20);(40;60);(60;40)}
11 tháng 12 2019
b. Bài làm :
Ta có : ƯCLN(a,b)=5
BCNN(a,b)=60
\(\Rightarrow\)ab=ƯCLN(a,b).BCNN(a,b)=5.60=300
Vì ƯCLN(a,b)=5 nên ta có : a=5m ; b=5n ; ƯCLN(m,n)=1 và m, n là các số tự nhiên
Mà ab=300
\(\Rightarrow\)5m.5n=300
\(\Rightarrow\)25m.n=300
\(\Rightarrow\)mn=12
Vì ƯCLN(m,n)=1 nên ta có bảng sau :
m 1 12 3 4
n 12 1 4 3
a 5 60 15 20
b 60 5 20 15
Vậy (a;b)\(\in\){(5;60);(60;5):(20;15):(15;20)}
a) Ta có: \(\hept{\begin{cases}\left[a,b\right]=120\\ab=1200\end{cases}}\Rightarrow\left(a,b\right)=ab\div\left[a,b\right]=1200\div120=10\)
Vì \(\left(a,b\right)=10\)nên \(\hept{\begin{cases}a=10m\\b=10n\\\left(m,n\right)=1\end{cases}}\)
Mà \(ab=1200\)
\(\Rightarrow10m.10n=1200\)
\(\Rightarrow100m.n=1200\)
\(\Rightarrow mn=12\)
Lại có: \(\left(m,n\right)=1\)
Ta có bảng sau:
m 1 12 3 4
n 12 1 4 3
a 10 120 30 40
b 120 10 40 30
Vậy \(\left(a;b\right)\in\left\{\left(10;120\right);\left(120;10\right);\left(30;40\right);\left(40;30\right)\right\}\).
b) Ta có: \(3a=7b\)
\(\Rightarrow\frac{a}{7}=\frac{b}{3}\)
Đặt \(\frac{a}{7}=\frac{b}{3}=k\)
\(\Rightarrow\hept{\begin{cases}a=k.7\\b=k.3\end{cases}}\)
Vì \(\left(a,b\right)=18\) nên \(\left(7k,3k\right)=18\)
Mà \(\left(7,3\right)=1\)
\(\Rightarrow k=18\)
\(\Rightarrow\hept{\begin{cases}a=18.7=126\\b=18.3=54\end{cases}}\)
Vậy a = 126 và b = 54.