Tìm a,b,c biết parabol y= ax2 +bx +c tiếp xúc với (d) y = ax+b tại điểm (1;3)?
Mọi người giúp em vs ạ !!! Mai em kt r!! Em xin cảm ơn!!!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 12 2023
Sửa đề: cắt trục tung tại điểm có tung độ bằng -3
Thay x=0 và y=-3 vào (P), ta được:
\(a\cdot0^2+b\cdot0+c=-3\)
=>0+0+c=-3
=>c=-3
vậy: (P): \(y=ax^2+bx-3\)
Tọa độ đỉnh là I(-1;-4) nên ta có:
\(\left\{{}\begin{matrix}-\dfrac{b}{2a}=-1\\-\dfrac{b^2-4\cdot a\cdot\left(-3\right)}{4a}=-4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}b=2a\\\dfrac{b^2+12a}{4a}=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=2a\\\left(2a\right)^2+12a=16a\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}b=2a\\4a^2-4a=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=2a\\4a\left(a-1\right)=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}b=2a\\\left[{}\begin{matrix}a=0\left(loại\right)\\a-1=0\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=1\\b=2\end{matrix}\right.\)
CM
6 tháng 6 2019
(P) : y = ax2 + bx + c
Parabol có đỉnh I(1 ; 4) ⇒ –b/2a = 1 ⇒ b = –2a ⇒ 2a + b = 0.
Parabol đi qua I(1; 4) ⇒ 4 = a.12 + b . 1 + c ⇒ a + b + c = 4.
Paraol đi qua D(3; 0) ⇒ 0 = a.32 + b.3 + c ⇒ 9a + 3b + c = 0.
Giải hệ phương trình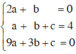 
ta được : a = –1 ; b = 2 ; c = 3.
Vậy a = –1 ; b = 2 ; c = 3.
CM
14 tháng 1 2017
(P): y = ax2 + bx + c
Parabol đi qua A(0 ; –1) ⇒ –1 = a.02 + b.0 + c ⇒ c = –1.
Parabol đi qua B(1 ; –1) ⇒ –1 = a.12 + b.1 + c ⇒ a + b + c = –1.
Mà c = –1 ⇒ a + b = 0 (1)
Parabol đi qua C(–1; 1) ⇒ a.(–1)2 + b.(–1) + c = 1 ⇒ a – b + c = 1.
Mà c = –1 ⇒ a – b = 2 (2)
Từ (1) và (2) ⇒ a = 1; b = –1.
Vậy a = 1 ; b = –1 ; c = –1.
3 tháng 2 2021
1, - Xét phương trình hoành độ giao điểm :\(2x^2=ax+b\)
\(\Rightarrow2x^2-ax-b=0\left(I\right)\)
Mà (P) tiếp xúc với d .
Nên PT ( I ) có duy nhất một nghiệm .
\(\Leftrightarrow\Delta=\left(-a\right)^2-4.2.\left(-b\right)=a^2+8b=0\)
Lại có : d đi qua A .
\(\Rightarrow b+0a=-2=b\)
\(\Rightarrow a=4\)
2. Tương tự a
3. - Xét phương trình hoành độ giao điểm :\(2x^2=2m+1\)
\(\Rightarrow2x^2-2m-1=0\)
Có : \(\Delta^,=\left(-m\right)^2-\left(-1\right).2=m^2+3\)
=> Giao điểm của P và d là : \(\left\{{}\begin{matrix}x_1=\dfrac{m+\sqrt{m^2+3}}{2}\\x_2=\dfrac{m-\sqrt{m^2+3}}{2}\end{matrix}\right.\)
CM
3 tháng 4 2018
Vì parabol đi qua ba điểm A, B, C nên ta có hệ phương trình:
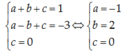
Vậy (P): y = -x2 + 2x
Chọn C.
Do (P) và (d) đều đi qua điểm (1;3) nên:
\(\left\{{}\begin{matrix}a+b+c=3\\a+b=3\end{matrix}\right.\) \(\Rightarrow c=0\)
Từ \(a+b=3\Rightarrow b=3-a\)
Vậy pt (d) và (P) lần lượt có dạng: \(\left\{{}\begin{matrix}y=ax^2+\left(3-a\right)x\\y=ax+3-a\end{matrix}\right.\)
Pt hoành độ giao điểm (P) và (d):
\(ax^2+\left(3-a\right)x=ax+3-a\)
\(\Leftrightarrow ax^2+\left(3-2a\right)x+a-3=0\) (1)
(P) tiếp xúc (d) khi và chỉ khi (1) có nghiệm kép
\(\Leftrightarrow\Delta=\left(3-2a\right)^2-4a\left(a-3\right)=0\)
\(\Leftrightarrow9=0\) (vô lý)
Vậy ko tồn tại a;b;c thỏa mãn yêu cầu đề bài