Xét chiều biến thiên của hàm số
\(y=2x-3\) khi \(x< -1\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
TXĐ: (-\infty; -1)\cup (-1;+\infty)$
$y'=\frac{1}{(x+1)^2}-2$
$y'>0\Leftrightarrow (x+1)^2< \frac{1}{2}\Leftrightarrow \frac{-1}{\sqrt{2}}-1< x< \frac{1}{\sqrt{2}}-1$
$y'< 0\Leftrightarrow (x+1)^2> \frac{1}{2}\Leftrightarrow x> \frac{1}{\sqrt{2}}-1$ hoặc $x< \frac{-1}{\sqrt{2}}-1$
Vậy hàm số:
Đồng biến trên $(\frac{-1}{\sqrt{2}}-1; \frac{1}{\sqrt{2}}-1)$ và nghịch biến trên $(\frac{1}{\sqrt{2}}-1; +\infty)\cup (-\infty; \frac{-1}{\sqrt{2}}-1)$

ta tính \(y'=3x^2-4x+1\)
\(y'=0\Rightarrow3x^2-4x+1=0\Rightarrow x=1;x=\frac{1}{3}\)
ta có
ta có trong khoảng 2 nghiệm thì y' cùng dấu với hệ số a, ngoài khoảng 2 nghiệm trái dấu với hệ số a
suy ra f'(x)>0 với \(x\in\left(-\infty;\frac{1}{3}\right)\cup\left(1;+\infty\right)\) suy ra hàm số đồng biến trên \(\left(-\infty;\frac{1}{3}\right)\cup\left(1;+\infty\right)\)
lại có f'(x)<0 với \(x\in\left(\frac{1}{3};1\right)\) suy ra hàm số nghịch biến trên \(\left(\frac{1}{3};1\right)\)

Hàm số y = 4 – 2x có:
+ Tập xác định D = R
+ Có a = –2 < 0 nên hàm số nghịch biến trên R.
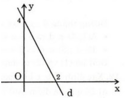
+ Tại x = 0 thì y = 4 ⇒ A(0 ; 4) thuộc đồ thị hàm số.
Tại x = 2 thì y = 0 ⇒ B(2; 0) thuộc đồ thị hàm số.
Vậy đồ thị hàm số là đường thẳng đi qua hai điểm A(0 ; 4) và B(2; 0).

a: TXĐ: D=R
Khi \(x\in D\Rightarrow-x\in D\)
\(f\left(-x\right)=-\left(-x\right)^2-2\cdot\left(-x\right)+3\)
\(=-x^2+2x+3\)
\(\Leftrightarrow f\left(-x\right)\ne f\left(x\right)\ne-f\left(x\right)\)
Vậy: Hàm số không chẵn không lẻ
Cái này là xét sự biến thiên: nghịch biến hay đồng biến chứ ạ???

Hàm số y = |x + 1|
Nếu x + 1 ≥ 0 hay x ≥ –1 thì y = x + 1.
Nếu x + 1 < 0 hay x < –1 thì y = –(x + 1) = –x – 1.
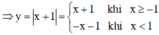
+ Tập xác định: R
+ Trên (–∞; –1), y = x + 1 đồng biến.
Trên (–1 ; +∞), y = –x – 1 nghịch biến.
Ta có bảng biến thiên :
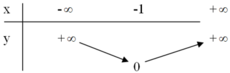
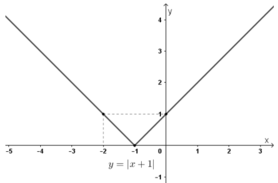
+ Đồ thị hàm số gồm hai phần:
Phần thứ nhất : Nửa đường thẳng y = x + 1 giữ lại các điểm có hoành độ ≥ –1.
Phần thứ hai : nửa đường thẳng y = –x – 1 giữ lại các điểm có hoành độ < –1.


Hàm số 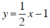 có:
có:
+ Tập xác định D = R.
+ Có 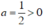 nên hàm số đồng biến trên R.
nên hàm số đồng biến trên R.
+ Tại x = 0 thì y = 1/2 . 0 – 1 = –1 . Vậy A (0; –1) thuộc đồ thị hàm số.
Tại x = 2 thì y = 1/2 . 2 – 1 = 0. Vậy B (2; 0) thuộc đồ thị hàm số.
Vậy đồ thị hàm số là đường thẳng đi qua hai điểm A (0; –1) và B (2; 0).
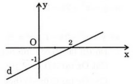
Do \(I=\frac{y_1-y_2}{x_1-x_2}=2>0\Rightarrow\) hàm số luôn đồng biến trên R
\(\Rightarrow\) hàm số luôn đồng biến trên \(\left(-\infty;-1\right)\)