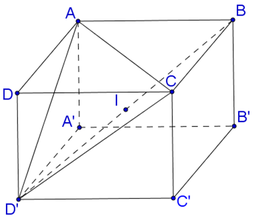
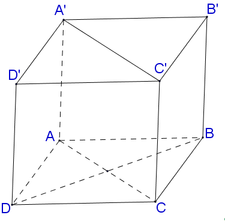
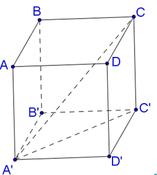
cho hình hộp ABCD.A'B'C'D'. gọi E trung điểm A'B'. Mp (P) qua E song song mp (CB'D') cắt C'D tại F. tính tỉ số \(\frac{DC'}{DF}\)?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án là C.
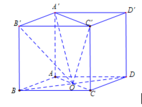
Ta có: V O . A , B , C , = 1 2 V O . A , B , C , D , ; V O . A , B , C , D , 1 3 V A B C D . A , B , C , D ,
V O . A , B , C , = 1 6 V A B C D . A , B , C , D , ⇒ V O . A , B , C , V A B C D . A , B , C , D = 1 6