Có bao nhiêu giá trị của m để giá trị nhỏ nhất của hàm số
f (x) = x2 + (2m+1)x +m2 -1 trên đoạn [0;1] bằng 1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đạo hàm f'(x) = m 2 - m + 1 ( x + 1 ) 2 > 0, ∀ x ∈ [ 0 ; 1 ]
Suy ra hàm số f(x) đồng biến trên [0; 1] nên min f(x) = f(0) = -m2+m
Theo bài ta có:
-m2+ m= -2 nên m= -1 hoặc m= 2.
Chọn D.

Ta có f ' x = - m 2 + m + 1 x + 1 2 > 0
Suy ra f(x) là hàm đồng biến trên [0;1]
Do đó f 0 ≤ f x ≤ f 1 hay
- m 2 + m ≤ f x ≤ 1 2 - m 2 + m + 1
Khi đó
m i n x ∈ 0 ; 1 f x = - m 2 + m = - 2 ⇔ m = - 1 m = 2
Đáp án A

Đáp án D
Xét hàm số ![]() .
.
![]() ;
;
![]()
![]()

Bảng biến thiên

Do ![]() nên
nên ![]() suy ra
suy ra ![]() .
.
Suy ra  .
.
Nếu ![]() thì
thì ![]() ,
, ![]()
![]()
![]()
![]() .
.
Nếu ![]() thì
thì ![]() ,
, ![]()
![]()
![]()
![]() .
.
Do đó ![]() hoặc
hoặc ![]() , do a nguyên và thuộc đoạn
, do a nguyên và thuộc đoạn ![]() nên
nên ![]() .
.

Chọn D
Điều kiện: x ≠ m
Hàm số đã cho xác định trên [0;4] khi ![]()
Ta có 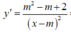
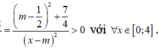
Hàm số đồng biến trên đoạn [0;4] nên 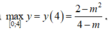
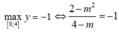
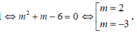
Kết hợp với điều kiện (*) ta được m = -3. Do đó có một giá trị của m thỏa yêu cầu bài toán.

Chọn đáp án D
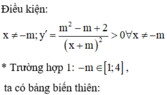
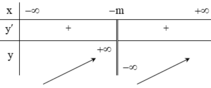


Vậy có đúng 1 giá trị của thỏa mãn điều kiện bài ra.


Đặt t= ex , với x ∈ [0 ; ln4] => t ∈ [1 ;4].
Khi đó f(x) = |t2 – 4t + m| = |g(t)|.
Có g’ (t) = 2t-4 và g’ (t) =0 khi t= 2.
Ta có bảng biến thiên
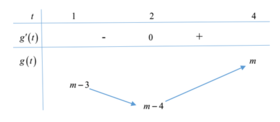
Từ bảng biến thiên ta thấy
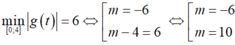
Chọn D.

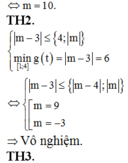
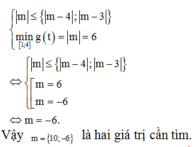





TH1: \(-\frac{b}{2a}=\frac{-2m-1}{2}\in\left[0;1\right]\)
\(\Leftrightarrow0\le\frac{-2m-1}{2}\le1\) \(\Leftrightarrow\) \(-\frac{3}{2}\le m\le-\frac{1}{2}\)
Khi đó \(f\left(x\right)_{min}=f\left(-\frac{b}{2a}\right)=f\left(\frac{-2m-1}{2}\right)=\frac{-4m-5}{4}\)
\(\Rightarrow-\frac{4m+5}{4}=1\Rightarrow m=-\frac{9}{4}\notin\left[-\frac{3}{2};-\frac{1}{2}\right]\) (loại)
TH2: \(-\frac{b}{2a}=\frac{-2m-1}{2}< 0\Leftrightarrow m>-\frac{1}{2}\)
Khi đó \(f\left(x\right)\) đồng biến trên \(\left[0;1\right]\Rightarrow f\left(x\right)_{min}=f\left(0\right)=m^2-1=1\)
\(\Rightarrow\left[{}\begin{matrix}m=-\sqrt{2}\left(l\right)\\m=\sqrt{2}\end{matrix}\right.\)
TH3: \(-\frac{b}{2a}=\frac{-2m-1}{2}>1\Leftrightarrow m< -\frac{3}{2}\)
Khi đó \(f\left(x\right)\) nghịch biến trên \(\left[0;1\right]\Rightarrow f\left(x\right)_{min}=f\left(1\right)=m^2+2m+1=1\)
\(\Rightarrow\left[{}\begin{matrix}m=0\left(l\right)\\m=-2\end{matrix}\right.\)
Vậy \(\left[{}\begin{matrix}m=-2\\m=\sqrt{2}\\\end{matrix}\right.\)
Cái đó thì bạn phải xem lại lý thuyết về hàm \(y=ax^2+bx+c\) khi \(a>0\) chứ
Hàm nghịch biến trên \(\left(-\infty;-\frac{b}{2a}\right)\) cũng như các tập con của nó
Hàm đồng biến trên \(\left(-\frac{b}{2a};+\infty\right)\) cũng như các tập con của nó