tìm x,y thỏa man: 2x+3y=19 và 1/3,x/y<1/2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TU
Tìm các số nguyên x, y thỏa mãn 2x + 3y =19 và \(\dfrac{1}{3}\) < \(\dfrac{x}{y}\)< \(\dfrac{1}{2}\)
2
30 tháng 9 2021
\(\dfrac{1}{3}< \dfrac{x}{y}< \dfrac{1}{2}\Rightarrow\dfrac{4}{12}< \dfrac{x}{y}< \dfrac{6}{12}\Rightarrow\dfrac{x}{y}=\dfrac{5}{12}\Rightarrow\dfrac{x}{5}=\dfrac{y}{12}\)
Áp dụng t/c dtsbn:
\(\dfrac{x}{5}=\dfrac{y}{12}=\dfrac{2x}{10}=\dfrac{3y}{36}=\dfrac{2x+3y}{10+36}=\dfrac{19}{46}\\ \Rightarrow\left\{{}\begin{matrix}x=\dfrac{95}{46}\\y=\dfrac{114}{23}\end{matrix}\right.\)
Mà \(x,y\in Z\)
Vậy ko có x,y nguyên thỏa mãn đề
DL
4
19 tháng 4 2020
a) \(\frac{2x}{3y}=\frac{-1}{3}\) và 2x + 3y = 7
Ta có : \(\frac{2x}{3y}=\frac{-1}{3}\Rightarrow\frac{2x}{-1}=\frac{3y}{3}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{2x}{-1}=\frac{3y}{3}=\frac{2x+3y}{\left(-1\right)+3}=\frac{7}{2}\)
=> \(\hept{\begin{cases}2x=\frac{7}{2}\cdot\left(-1\right)=-\frac{7}{2}\\3y=\frac{7}{2}\cdot3=\frac{21}{2}\end{cases}\Rightarrow}\hept{\begin{cases}x=\left(-\frac{7}{2}\right):2=-\frac{7}{4}\\y=\frac{21}{2}:3=\frac{7}{2}\end{cases}}\)
b) 21x = 19y => \(\frac{21x}{399}=\frac{19y}{399}\)=> \(\frac{x}{19}=\frac{y}{21}\)
Áp dụng t/c dãy tỉ số = nhau ta có :
\(\frac{x}{19}=\frac{y}{21}=\frac{x-y}{19-21}=\frac{4}{-2}=-2\)
=> x = -38,y = -42
19 tháng 4 2020
\(a,\frac{2x}{3y}=-\frac{1}{3}\)và \(2x+3y=7\)
Theo bài ra ta có
\(\frac{2x}{3y}=-\frac{1}{3}\Rightarrow\frac{2x}{-1}=\frac{3y}{3}\)
Áp dụng dãy tỉ số bằng nhau ta có
\(\frac{2x}{-1}=\frac{3y}{3}=\frac{2x+3y}{-1+3}=\frac{7}{2}\)
\(\hept{\begin{cases}\frac{2x}{-1}=\frac{7}{2}\\\frac{3y}{3}=\frac{7}{2}\end{cases}\Rightarrow\hept{\begin{cases}2x=-\frac{7}{2}\\3y=\frac{21}{2}\end{cases}\Rightarrow}\hept{\begin{cases}x=-\frac{7}{4}\\y=\frac{7}{2}\end{cases}}}\)
\(b,21x=19y\)và \(x-y=4\)
Theo bài ra ta có
\(21x=19y\Rightarrow\frac{x}{19}=\frac{y}{21}\)
Áp dụng dãy tỉ số bằng nhau ta có
\(\frac{x}{19}=\frac{y}{21}=\frac{x-y}{19-21}=\frac{4}{-2}=-2\)
\(\hept{\begin{cases}\frac{x}{19}=-2\\\frac{y}{21}=-2\end{cases}\Rightarrow\hept{\begin{cases}x=-38\\y=-42\end{cases}}}\)
22 tháng 8 2020
\(\hept{\begin{cases}\frac{x}{2}=\frac{y}{3}=3z\\2x-3y+4z=1\end{cases}}\Rightarrow\hept{\begin{cases}\frac{x}{2}=\frac{y}{3}=\frac{z}{\frac{1}{3}}\\2x-3y+4z=1\end{cases}}\Rightarrow\hept{\begin{cases}\frac{2x}{4}=\frac{3y}{9}=\frac{4z}{\frac{4}{3}}\\2x-3y+4z=1\end{cases}}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{2x}{4}=\frac{3y}{9}=\frac{4z}{\frac{4}{3}}=\frac{2x-3y+4z}{4-9+\frac{4}{3}}=\frac{1}{-\frac{11}{3}}=-\frac{3}{11}\)
\(\frac{2x}{4}=-\frac{3}{11}\Rightarrow x=-\frac{6}{11}\)
\(\frac{3y}{9}=-\frac{3}{11}\Rightarrow y=-\frac{9}{11}\)
\(\frac{4z}{\frac{4}{3}}=-\frac{3}{11}\Rightarrow z=-\frac{1}{11}\)
Vậy ...
22 tháng 8 2020
\(\frac{x}{2}=\frac{y}{3}=3z\Rightarrow\frac{x}{2}=\frac{y}{3}=\frac{z}{\frac{1}{3}}\)
Áp dụng tính chất dãy tỉ số bằng nhau :
\(\frac{x}{2}=\frac{y}{3}=\frac{z}{\frac{1}{3}}=\frac{2x-3y+4z}{2\cdot2-3\cdot3+4\cdot\frac{1}{3}}=\frac{1}{-\frac{11}{3}}=-\frac{3}{11}\)
\(\frac{x}{2}=-\frac{3}{11}\Rightarrow x=-\frac{3}{11}\cdot2=-\frac{6}{11}\)
\(\frac{y}{3}=-\frac{3}{11}\Rightarrow y=-\frac{3}{11}\cdot3=-\frac{9}{11}\)
\(\frac{z}{\frac{1}{3}}=-\frac{3}{11}\Rightarrow z=-\frac{3}{11}\cdot\frac{1}{3}=-\frac{1}{11}\)
28 tháng 10 2023
4:
(x+1)(y-2)=5
=>\(\left(x+1;y-2\right)\in\left\{\left(1;5\right);\left(5;1\right);\left(-1;-5\right);\left(-5;-1\right)\right\}\)
=>\(\left(x,y\right)\in\left\{\left(0;7\right);\left(4;3\right);\left(-2;-3\right);\left(-6;1\right)\right\}\)
30 tháng 8 2015
x^2 + 3xy + 2y^2 = 0
=> x^2 + xy + 2xy + 2y^2 = 0
=> x(x+y) + 2y ( x+ y ) = 0 =
=> ( x+ 2y)( x + y ) = 0
=> x = -2y hoặc x = -y
(+) x = -2y thay vào ta có :
8y^2 + 6y + 5 = 0 giải ra y => x
(+) thay x = -y ta có :
2y^2 - 3y + 5 = 0 tương tự
KY
19 tháng 9 2019
a) \(M=\left(x^2+\frac{1}{y^2}\right)\left(y^2+\frac{1}{x^2}\right)=x^2\left(y^2+\frac{1}{x^2}\right)\)
\(+\frac{1}{y^2}\left(y^2+\frac{1}{x^2}\right)=x^2y^2+2+\frac{1}{x^2y^2}\)
\(=2+\left(x^2y^2+\frac{1}{256x^2y^2}\right)+\frac{255}{256x^2y^2}\)
Áp dụng BĐT Cauchy - Schwar cho 2 số không âm, ta được:
\(x^2y^2+\frac{1}{256x^2y^2}\ge2\sqrt{\frac{x^2y^2}{256x^2y^2}}=\frac{1}{8}\)
C/m được BĐT phụ: \(1=\left(x+y\right)^2\ge4xy\)
\(\Leftrightarrow16x^2y^2\le1\Leftrightarrow256x^2y^2\le16\Leftrightarrow\frac{255}{256x^2y^2}\ge\frac{255}{16}\)
\(\Rightarrow M\ge2+\frac{1}{8}+\frac{255}{16}=\frac{289}{16}\)
(Dấu "="\(\Leftrightarrow\hept{\begin{cases}x^2y^2=\frac{1}{256x^2y^2}\\x-y=0\end{cases}}\Leftrightarrow x=y=\frac{1}{2}\))
19 tháng 9 2019
\(\frac{16}{3x+3y+2z}=\frac{16}{\left(x+y\right)+\left(y+z\right)+\left(z+x\right)+\left(x+y\right)1}\le\frac{1}{x+y}+\frac{1}{y+z}+\frac{1}{z+x}+\frac{1}{x+y}\)
Tương tự \(\frac{16}{3x+2y+3z}\le\frac{1}{x+y}+\frac{1}{y+z}+\frac{1}{z+x}+\frac{1}{x+z}\)
\(\frac{16}{2x+3y+3z}\le\frac{1}{x+y}+\frac{1}{y+z}+\frac{1}{z+x}+\frac{1}{y+z}\)
Cộng vế theo vế ta có:
\(16\left(\frac{1}{3x+2y+3z}+\frac{1}{3x+3y+2z}+\frac{1}{2x+3y+3z}\right)\le4\left(\frac{1}{x+y}+\frac{1}{y+z}+\frac{1}{z+x}\right)=24\)
\(\Rightarrow\frac{1}{3x+3y+2z}+\frac{1}{3x+2y+3z}+\frac{1}{2x+3y+3z}\le\frac{3}{2}\left(đpcm\right)\)
P/S:Có dùng S-vác ngược dấu ạ.ý tưởng tách mẫu là từ tth_new - Trang của tth_new - Học toán với OnlineMath nha !
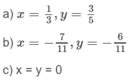
x là một số nào đó trong dãy số tuwh nhiên và y cũng như vậy
bạn ghi câu trên vào vở đi mình không nói dối đâu thật đó mình học rồi nên mình biết
Ko biết Anh ơi