Cho tam giác ABC. Xác định điểm F thỏa mãn đẳng thức \(\overrightarrow{FA}+\overrightarrow{FB}+\overrightarrow{FC}=\overrightarrow{AB}+\overrightarrow{AC}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
24 tháng 9 2023
a) Ta có: \(\overrightarrow {AC} = \frac{1}{2}\overrightarrow {AB} \)
\( \Rightarrow \)Hai vecto \(\overrightarrow {AB} ,\overrightarrow {AC} \) cùng hướng và \(AC = \frac{1}{2}AB\).
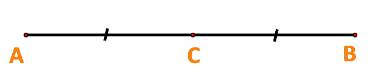
Vậy C là trung điểm của AB.
b) Ta có: \(\overrightarrow {AD} = - \frac{1}{2}\overrightarrow {AB} = - \overrightarrow {AC} \)
\( \Rightarrow \)Hai vecto \(\overrightarrow {AD} ,\overrightarrow {AC} \) ngược hướng và \(AD = AC\).
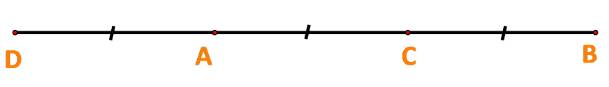
Vậy A là trung điểm DC.
15 tháng 11 2021
\(a,\) \(\overrightarrow{IA}=2\overrightarrow{IB}-4\overrightarrow{IC}\)
\(\overrightarrow{IA}=2\overrightarrow{IB}-2\overrightarrow{IC}-2\overrightarrow{IC}=2\overrightarrow{CB}-2\overrightarrow{IC}\)
\(=2\left(\overrightarrow{AB}-\overrightarrow{AC}\right)-2\left(\overrightarrow{AC}-\overrightarrow{AI}\right)\)
\(\overrightarrow{IA}=2\overrightarrow{AB}-2\overrightarrow{AC}-2\overrightarrow{AC}+2\overrightarrow{AI}\)
\(\overrightarrow{IA}=\dfrac{2}{3}\overrightarrow{AB}-\dfrac{4}{3}\overrightarrow{AC}\)
\(b,\overrightarrow{IJ}=\overrightarrow{AJ}-\overrightarrow{AI}=\dfrac{2}{3}\overrightarrow{AB}+\overrightarrow{IA}=\dfrac{2}{3}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AB}-\dfrac{4}{3}\overrightarrow{AC}=\dfrac{4}{3}\left(\overrightarrow{AB}-\overrightarrow{AC}\right)\left(1\right)\)
\(\overrightarrow{JG}=\overrightarrow{AG}-\overrightarrow{AJ}=\dfrac{2}{3}\overrightarrow{AM}-\dfrac{2}{3}\overrightarrow{AB}\)\((\) \(\) \(M\) \(trung\) \(điểm\) \(BC)\)
\(\overrightarrow{JG}=\dfrac{\overrightarrow{AB}+\overrightarrow{AC}}{3}-\dfrac{2}{3}\overrightarrow{AB}=-\dfrac{1}{3}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}=-\dfrac{1}{3}\left(\overrightarrow{AB}-\overrightarrow{AC}\right)\left(2\right)\)
\(\left(1\right)\left(2\right)\Rightarrow\overrightarrow{IJ}=-4\overrightarrow{JG}\Rightarrow I,J,G\) \(thẳng\) \(hàng\)
HP
17 tháng 12 2020
a, \(\left(\overrightarrow{AC}-\overrightarrow{AB}\right)^2=\overrightarrow{BC}^2\)
\(\Leftrightarrow AC^2+AB^2-2\overrightarrow{AB}.\overrightarrow{AC}=BC^2\)
\(\Leftrightarrow2\overrightarrow{AB}.\overrightarrow{AC}=AB^2+AC^2-BC^2\)
\(\Rightarrow\overrightarrow{AB}.\overrightarrow{AC}=\dfrac{AB^2+AC^2-BC^2}{2}=\dfrac{5^2+8^2-7^2}{2}=20\)
b, \(2\overrightarrow{CA}.\overrightarrow{CB}=CA^2+CB^2-BC^2=CA^2\)
\(\Rightarrow\overrightarrow{CA}.\overrightarrow{CB}=\dfrac{CA^2}{2}=\dfrac{8^2}{2}=32\)
AH
Akai Haruma
Giáo viên
17 tháng 12 2020
Lời giải:
a)
\(\overrightarrow{AC}-\overrightarrow{AB}=\overrightarrow{BC}\)
\(\Rightarrow (\overrightarrow{AC}-\overrightarrow{AB})^2=\overrightarrow{BC}^2\Leftrightarrow AB^2+AC^2-2\overrightarrow{AC}.\overrightarrow{AB}=BC^2\)
\(\Leftrightarrow 2\overrightarrow{AB}.\overrightarrow{AC}=AB^2+AC^2-BC^2\) (đpcm)
Ta có:
\(\overrightarrow{AB}.\overrightarrow{AC}=\frac{AB^2+AC^2-BC^2}{2}=\frac{5^2+8^2-7^2}{2}=20\)
\(\cos \angle A=\frac{\overrightarrow{AB}.\overrightarrow{AC}}{|\overrightarrow{AB}|.|\overrightarrow{AC}|}=\frac{20}{5.8}=\frac{1}{2}\)
\(\Rightarrow \angle A=60^0\)
b)
Tương tự phần a, \(\overrightarrow{CA}.\overrightarrow{CB}=\frac{CA^2+CB^2-AB^2}{2}=\frac{8^2+7^2-5^2}{2}=44\)
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 11 2021
1.
\(\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{AI}=\overrightarrow{0}\Leftrightarrow\overrightarrow{IB}+\overrightarrow{AC}=0\)
\(\Leftrightarrow\overrightarrow{IB}=\overrightarrow{CA}\)
\(\Rightarrow\) I là 1 đỉnh của hình bình hành ABIC
2.
Gọi N là trung điểm AB \(\Rightarrow\overrightarrow{AN}=\dfrac{1}{2}\overrightarrow{AB}\)
\(\overrightarrow{MA}+\overrightarrow{BM}+2\overrightarrow{MC}=\overrightarrow{0}\Leftrightarrow\overrightarrow{BA}+2\overrightarrow{MC}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{MC}=\dfrac{1}{2}\overrightarrow{AB}\Leftrightarrow\overrightarrow{MC}=\overrightarrow{AN}\)
\(\Rightarrow\) M là 1 đỉnh của hình bình hành ANCM
HT
17 tháng 2 2021
1/ \(\overrightarrow{AM}=3\overrightarrow{AM}+\overrightarrow{MB}+\overrightarrow{MC}+\overrightarrow{MD}\)
\(\Leftrightarrow2\overrightarrow{AM}+3\overrightarrow{MG}=\overrightarrow{0}\)
\(\Leftrightarrow2\overrightarrow{AM}+3\overrightarrow{MA}+3\overrightarrow{AG}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{AM}=3\overrightarrow{AG}\)
Ban tu ket luan
2/ Bạn coi lại đề bài, đẳng thức kia có vấn đề. 2k-1IB??
17 tháng 2 2021
\(\overrightarrow{IA}+2k-1+\overrightarrow{IB}+k\overrightarrow{IC}+\overrightarrow{ID}=0\)
HQ
Hà Quang Minh
Giáo viên
24 tháng 9 2023
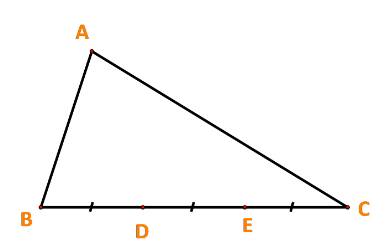
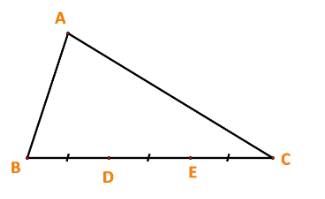
Ta có: \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \Leftrightarrow \overrightarrow {BC} = \overrightarrow b - \overrightarrow a \)
Lại có: vecto \(\overrightarrow {BD} ,\overrightarrow {BC} \) cùng hướng và \(\left| {\overrightarrow {BD} } \right| = \frac{1}{3}\left| {\overrightarrow {BC} } \right|\)
\( \Rightarrow \overrightarrow {BD} = \frac{1}{3}\overrightarrow {BC} = \frac{1}{3}(\overrightarrow b - \overrightarrow a )\)
Tương tự: vecto \(\overrightarrow {BE} ,\overrightarrow {BC} \) cùng hướng và \(\left| {\overrightarrow {BE} } \right| = \frac{2}{3}\left| {\overrightarrow {BC} } \right|\)
\( \Rightarrow \overrightarrow {BE} = \frac{2}{3}\overrightarrow {BC} = \frac{2}{3}(\overrightarrow b - \overrightarrow a )\)
Ta có:
\(\overrightarrow {AB} + \overrightarrow {BD} = \overrightarrow {AD} \Leftrightarrow \overrightarrow {AD} = \overrightarrow a + \frac{1}{3}(\overrightarrow b - \overrightarrow a ) = \frac{2}{3}\overrightarrow a + \frac{1}{3}\overrightarrow b \)
\(\overrightarrow {AB} + \overrightarrow {BE} = \overrightarrow {AE} \Leftrightarrow \overrightarrow {AE} = \overrightarrow a + \frac{2}{3}(\overrightarrow b - \overrightarrow a ) = \frac{1}{3}\overrightarrow a + \frac{2}{3}\overrightarrow b \)