cho tam giác ABC vuông tại A có AB =3cm . BC=5cm . đường cao AH
a , tính số đo góc B, C ,tính AH, AC
b. gọi AE là phân giác của góc A (E thuộc BC) tính AE
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
a: Xét ΔBAC vuông tại A có
\(\widehat{B}+\widehat{C}=90^0\)
hay \(\widehat{C}=60^0\)
Xét ΔBAC vuông tại A có
\(AB=BC\cdot\sin60^0\)
\(\Leftrightarrow BC=4\sqrt{3}\left(cm\right)\)
\(\Leftrightarrow AC=2\sqrt{3}\left(cm\right)\)

a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=3^2+4^2=25\)
hay BC=5(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH\cdot BC=AB\cdot AC\)
\(\Leftrightarrow AH\cdot5=3\cdot4=12\)
hay AH=2,4(cm)
b) Xét ΔABC vuông tại A có
\(\sin\widehat{B}=\dfrac{AC}{BC}=\dfrac{4}{5}\)
hay \(\widehat{B}\simeq53^0\)
\(\Leftrightarrow\widehat{C}=37^0\)
c) Xét ΔABC có AE là đường phân giác ứng với cạnh BC(gt)
nên \(\dfrac{BE}{AB}=\dfrac{CE}{AC}\)(Tính chất tia phân giác của tam giác)
hay \(\dfrac{BE}{3}=\dfrac{CE}{4}=\dfrac{BE+CE}{3+4}=\dfrac{5}{7}\)
Do đó:
\(\left\{{}\begin{matrix}BE=\dfrac{15}{7}\left(cm\right)\\CE=\dfrac{20}{7}\left(cm\right)\end{matrix}\right.\)

a) Xét tam giác ABC vuông tại A có AB=3 cm; BC= 5 cm
=> AB\(^2\)+BC\(^2\)=AC\(^2\)
= 3\(^2\)+5\(^2\) =AC\(^2\)
=9 + 25= AC\(^2\)
=> 34 = AC\(^2\)
=> \(\sqrt{34}\)= AC
Vậy AC = \(\sqrt{34}\) cm
1) Áp dụng định lí Py-ta-go vào tam giác ABC:
BC2= AB2+ AC2
--> AC2= BC2 - AB2= 52 - 32= 25- 9 = 16
\(\Rightarrow\)AC = \(\sqrt{16}=4\) (cm)
2) Xét \(\Delta\)BAD và \(\Delta\)BHD :
BAD=BHD=90o
BD chung
ABD=HBD
\(\Rightarrow\) \(\Delta\)BAD = \(\Delta\)BHD (cạnh huyền_góc nhọn)
\(\Rightarrow\)BA=BH (2 cạnh t/ứng)
\(\Rightarrow\)B cách đều 2 đầu mút của đoạn AH \(\Rightarrow\) BH vuông góc với AH
3) ko biết

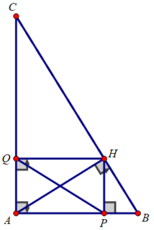
b)Xét tam giác ABC vuông tại A có:
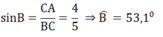
∠B + ∠C = 90 0 ⇒ ∠C = 90 0 - 53 , 1 0 = 36 , 9 0
Xét tứ giác APHQ có:
∠(PAQ) = ∠(AQH) = ∠(APH) = 90 0
⇒ Tứ giác APHQ là hình chữ nhật
⇒ PQ = AH = 12/5 (cm)

Xét \(\Delta BAC\) Và \(\Delta ACH\) có :
\(\widehat{BAC}\)\(=\)\(\widehat{AHC}\) ( cùng = 900 )
\(\widehat{C}\)là góc chung
\(\Rightarrow\) \(\Delta BAC\)\(~\)\(\Delta AHC\) ( g - g ) (1)
\(\Rightarrow\)\(\frac{BC}{AC}=\frac{AB}{AH}\)\(\Rightarrow BC.AH=AB.AC\)
b) Xét \(\Delta AHC\)có :
K là trung điểm của CH
I là trung điểm của AH
\(\Rightarrow\)IK // AC
Do IK // AC :
\(\Rightarrow\)\(\Delta HIK\)\(~\)\(\Delta HAC\) (2)
Từ (1) và (2) =) \(\Delta HIK\)\(~\)\(\Delta ABC\)
Do \(HE\)\(\perp\)\(AB\)\(\Rightarrow\)\(\widehat{A\text{E}H}\)= 900
\(HF\)\(\perp\)\(AC\)\(\Rightarrow\)\(\widehat{FHE}\)= 900
Xét tứ giác AEHF có:
\(\widehat{BAC}=\widehat{A\text{E}H}=\widehat{FHE}\)\(=90^0\)
\(\Rightarrow\)AEHF là hình chữ nhật \(\Rightarrow\) AE = HF
Xét \(\Delta ABC\)\(\perp\)tại \(A\)
Áp dụng định lí py - ta - go
BC2 = AB2 + AC2
52 = 32 + AC2
AC2 = 16
AC = 4 ( cm )
Ta có ; \(S_{\Delta ABC}\)\(=\frac{AB.AC}{2}\)\(=\frac{3.4}{2}=6\)cm2
\(S_{\Delta ABC}=\frac{1}{2}.BC.AH\)\(=\frac{1}{2}.5.AH=2,5.AH\)
\(\Rightarrow2,5.AH=6\)\(\Rightarrow AH=2,4\)cm
Xét \(\Delta AHC\)\(\perp\)tại A
Áp dụng định lí py - ta - go
AC2 = AH2 + HC2
42 = (2,4)2 + CH2
CH2 = 10,24
CH = 3,2 cm
Ta có : \(S_{\Delta AHC}=\frac{AH.AC}{2}=\)\(\frac{2,4.3,2}{2}=3,84\)cm2
\(S_{\Delta AHC}=\frac{1}{2}.AC.HF\)\(=\frac{1}{2}.4.HF=2.HF\)
\(\Rightarrow\)2.HF = 3.84
HF = 1.92 cm
\(\Rightarrow A\text{E}=1,92\)( Vì HF = AE , cmt)

a: Xét ΔABC vuông tại A và ΔHAC vuông tại H có
góc C chung
=>ΔABC đồng dạg với ΔHAC
b: BC=căn 3^2+4^2=5cm
AH=3*4/5=2,4cm
c: góc ADE=90 độ-góc ABD
góc AED=góc BEH=90 độ-góc DBC
mà góc ABD=góc DBC
nên góc ADE=góc AED
=>AD=AE

a: Xét ΔABC vuông tại A và ΔHAC vuông tại H có
góc C chung
=>ΔABC đồng dạng với ΔHAC
b: BC=căn 3^2+4^2=5cm
AH=3*4/5=2,4cm
c: góc AED=góc BEH=90 độ-góc DBC
góc ADE=90 độ-góc ABD
mà góc DBC=góc ABD
nên góc AED=góc ADE
=>AD=AE
Tự vẽ hình:
a) Ta có: Áp dụng định lý Pytago:
\(AB^2+AC^2=BC^2\)
\(\Rightarrow AC^2=BC^2-AB^2=5^2-3^2=16=4^2\)
\(\Rightarrow AC=4\left(cm\right)\)
Từ đó ta dễ dàng tính được: \(AH.BC=AB.AC\)
\(\Rightarrow AH=\frac{AB.AC}{BC}=\frac{3.4}{5}=\frac{12}{5}\left(cm\right)\)