cmr trong 2 số dương thì số nào lớn hơn thì có bình phương lớn hơn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


mình nghĩ là thế này
a)Nhân hai vế của x>y với số dương x được x^2>xy(1)
Nhân hai vế của x>y với số dương y được xy>y^2(2)
Từ (1) và (2) suy ra:
x^2>y^2

bạn vào olm.vn/hoi-đap/691595 , câu hỏi của 'mãi mãi là em ' nha. mik thấy có bạn trả lời rồi đó

Cho x>y>0.
Nhân hai vế của x>y với số dương x ta được x2>xy (1)
Nhân 2 vế của x>y với số dương y ta được xy>y2 (2)
Từ (1) và (2) =>x2>y2

Độ lệch chuẩn bằng căn bậc hai của phương sai.
=> Mẫu nào có phương sai lớn hơn thì có độ lệch chuẩn lớn hơn.
Chọn A.

Đặt lại yêu cầu đề bài :
So sánh hai phân số \(\frac{a}{b}\) và \(\frac{a}{c}\) với a, b, c \(\in\) N* và b < c.
Ta có \(\frac{a}{b}=\frac{ac}{bc}\) ; \(\frac{a}{c}=\frac{ab}{bc}\)
Do b < c và a > 0 nên ab < ac.
Vậy \(\frac{ac}{bc}>\frac{ab}{bc}\) tức là \(\frac{a}{b}>\frac{a}{c}\).
suy ra điều phải chứng minh.
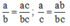
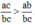
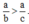
số lớn hơn thì bình phương của nó bàng số lớn hơn nhân vớ số lớn hơn đó thì có cũng vẫn lớn hơn