tìm GTNN của hàm số
y=3(sinx-cosx)+4sinxcosx \(\forall x\in\left\{\frac{-\Pi}{2};0\right\}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
6 tháng 8 2021
2.
$y=\sin ^4x+\cos ^4x=(\sin ^2x+\cos ^2x)^2-2\sin ^2x\cos ^2x$
$=1-\frac{1}{2}(2\sin x\cos x)^2=1-\frac{1}{2}\sin ^22x$
Vì: $0\leq \sin ^22x\leq 1$
$\Rightarrow 1\geq 1-\frac{1}{2}\sin ^22x\geq \frac{1}{2}$
Vậy $y_{\max}=1; y_{\min}=\frac{1}{2}$
AH
Akai Haruma
Giáo viên
6 tháng 8 2021
3.
$0\leq |\sin x|\leq 1$
$\Rightarrow 3\geq 3-2|\sin x|\geq 1$
Vậy $y_{\min}=1; y_{\max}=3$
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 7 2020
a/
\(y=\frac{1}{sinx}+\frac{1}{cosx}\ge\frac{4}{sinx+cosx}=\frac{4}{\sqrt{2}sin\left(x+\frac{\pi}{4}\right)}\ge\frac{4}{\sqrt{2}}=2\sqrt{2}\)
\(y_{min}=2\sqrt{2}\) khi \(\left\{{}\begin{matrix}sinx=cosx\\sin\left(x+\frac{\pi}{4}\right)=1\end{matrix}\right.\) \(\Rightarrow x=\frac{\pi}{4}\)
\(y_{max}\) không tồn tại (y dần tới dương vô cùng khi x gần tới 0 hoặc \(\frac{\pi}{2}\))
b/
\(y=\frac{1}{1-cosx}+\frac{1}{1+cosx}=\frac{1+cosx+1-cosx}{1-cos^2x}=\frac{2}{sin^2x}\)
Hàm số ko tồn tại cả min lẫn max ( \(0< y< \infty\))
c/
Do \(tan^2x\) ko tồn tại max (tiến tới vô cực) trên khoảng đã cho nên hàm ko tồn tại max
\(y=2+\frac{sin^4x+cos^4x}{\left(sinx.cosx\right)^2}+\frac{1}{sin^4x+cos^4x}\ge2+2\sqrt{\frac{sin^4x+cos^4x}{\frac{1}{4}sin^22x.\left(sin^4x+cos^4x\right)}}\)
\(y\ge2+\frac{4}{sin2x}\ge2+\frac{4}{1}=6\)
\(y_{min}=6\) khi \(\left\{{}\begin{matrix}sin2x=1\\sin^4x+cos^4x=sinx.cosx\end{matrix}\right.\) \(\Rightarrow x=\frac{\pi}{4}\)
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
a) Vẽ đồ thị:
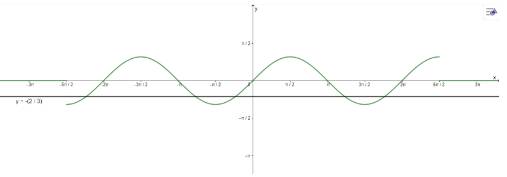
\(3\sin x + 2 = 0\) trên đoạn \(\left( { - \frac{{5\pi }}{2};\frac{{5\pi }}{2}} \right)\) có 5 nghiệm
b) Vẽ đồ thị:
\(\cos x = 0\) trên đoạn \(\left[ { - \frac{{5\pi }}{2};\frac{{5\pi }}{2}} \right]\) có 6 nghiệm
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
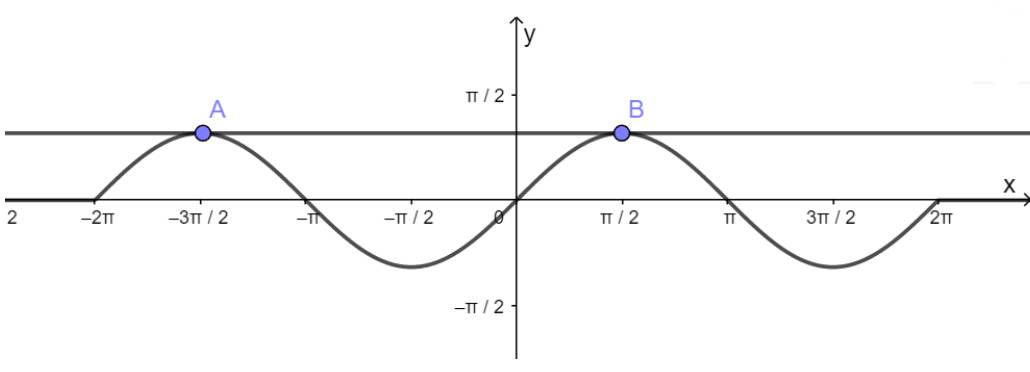
a) Hàm số y = sinx nhận giá trị bằng 1
- Vẽ hàm số y = sinx trên đoạn \(\left[ { - 2\pi ;2\pi } \right]\)
- Vẽ hàm số y = 1
- Lấy giao điểm của hai hàm số y = sinx và y = 1 là A, B,...
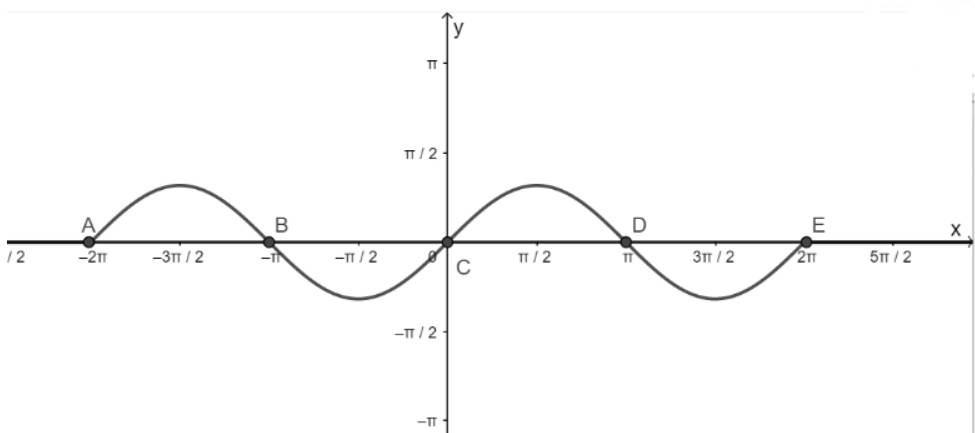
b) Hàm số y = sinx nhận giá trị bằng 0
- Vẽ hàm số y = sinx trên đoạn \(\left[ { - 2\pi ;2\pi } \right]\)
- Vẽ hàm số y = 0
- Lấy giao điểm của hai hàm số y = sinx và y = 0 là A, B, C, D, E,...
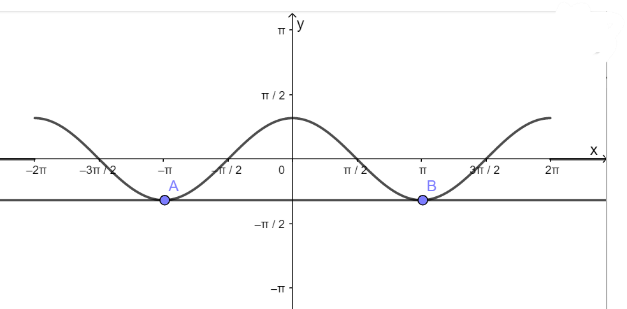
c) Hàm số y = cosx nhận giá trị bằng – 1
- Vẽ hàm số y = cosx trên đoạn \(\left[ { - 2\pi ;2\pi } \right]\)
- Vẽ hàm số y = - 1
- Lấy giao điểm của hai hàm số y = cosx và y = - 1 là A, B,...
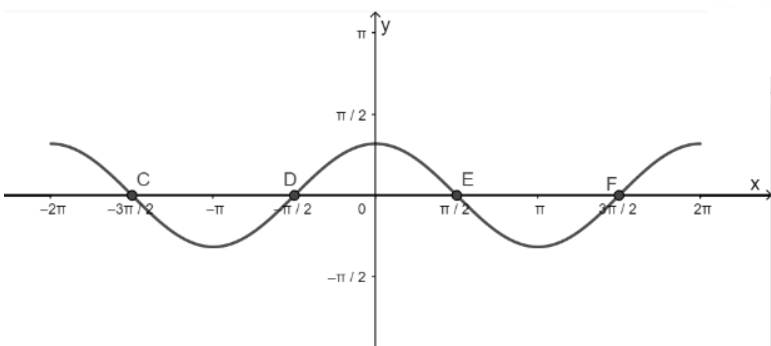
d) Hàm số y = cosx nhận giá trị bằng 0
- Vẽ hàm số y = cosx trên đoạn \(\left[ { - 2\pi ;2\pi } \right]\)
- Vẽ hàm số y = 0
- Lấy giao điểm của hai hàm số y = cosx và y = 0 là C, D, E, F,...
14 tháng 8 2023
a: ĐKXĐ: 2*sin x+1<>0
=>sin x<>-1/2
=>x<>-pi/6+k2pi và x<>7/6pi+k2pi
b: ĐKXĐ: \(\dfrac{1+cosx}{2-cosx}>=0\)
mà 1+cosx>=0
nên 2-cosx>=0
=>cosx<=2(luôn đúng)
c ĐKXĐ: tan x>0
=>kpi<x<pi/2+kpi
d: ĐKXĐ: \(2\cdot cos\left(x-\dfrac{pi}{4}\right)-1< >0\)
=>cos(x-pi/4)<>1/2
=>x-pi/4<>pi/3+k2pi và x-pi/4<>-pi/3+k2pi
=>x<>7/12pi+k2pi và x<>-pi/12+k2pi
e: ĐKXĐ: x-pi/3<>pi/2+kpi và x+pi/4<>kpi
=>x<>5/6pi+kpi và x<>kpi-pi/4
f: ĐKXĐ: cos^2x-sin^2x<>0
=>cos2x<>0
=>2x<>pi/2+kpi
=>x<>pi/4+kpi/2
HP
29 tháng 8 2021
a, Đồ thị hàm số \(y=cosx\): \(\left(A=\left(-\dfrac{\pi}{2};0\right);B=\left(\dfrac{\pi}{2};0\right)\right)\)
Dựa vào đồ thị ta có \(\left\{{}\begin{matrix}y_{min}=0\\y_{max}=1\end{matrix}\right.\)
b, Đồ thị hàm số \(y=sinx\): \(\left(A=\left(-\dfrac{\pi}{2};-1\right);A=\left(\dfrac{\pi}{2};1\right)\right)\)
C
1
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 1 2024
\(\Leftrightarrow m.cosx+\left(2m-1\right)sinx+3-m=y\left(cosx+sinx-2\right)\)
\(\Leftrightarrow\left(m-y\right)cosx+\left(2m-y-1\right)sinx=m-2y-3\)
Pt có nghiệm khi:
\(\left(m-y\right)^2+\left(2m-y-1\right)^2\ge\left(m-2y-3\right)^2\)
\(\Leftrightarrow2y^2+\left(2m+10\right)y-4m^2-2m+8\le0\)
\(\Rightarrow\dfrac{-m-5-\sqrt{9m^2+14m+9}}{2}\le y\le\dfrac{-m-5+\sqrt{9m^2+14m+9}}{2}\)
\(\Rightarrow y_{min}=\dfrac{-m-5-\sqrt{9m^2+14m+9}}{2}\le3\)
\(\Rightarrow\sqrt{9m^2+14m+9}\ge-m-11\)
BPT này đúng với mọi m. Vậy bài toán thỏa mãn với mọi m
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
a) y = sinx
- Khoảng \(\left( { - \frac{{9\pi }}{2}; - \frac{{7\pi }}{2}} \right)\)
+ Vẽ đồ thị hàm số:
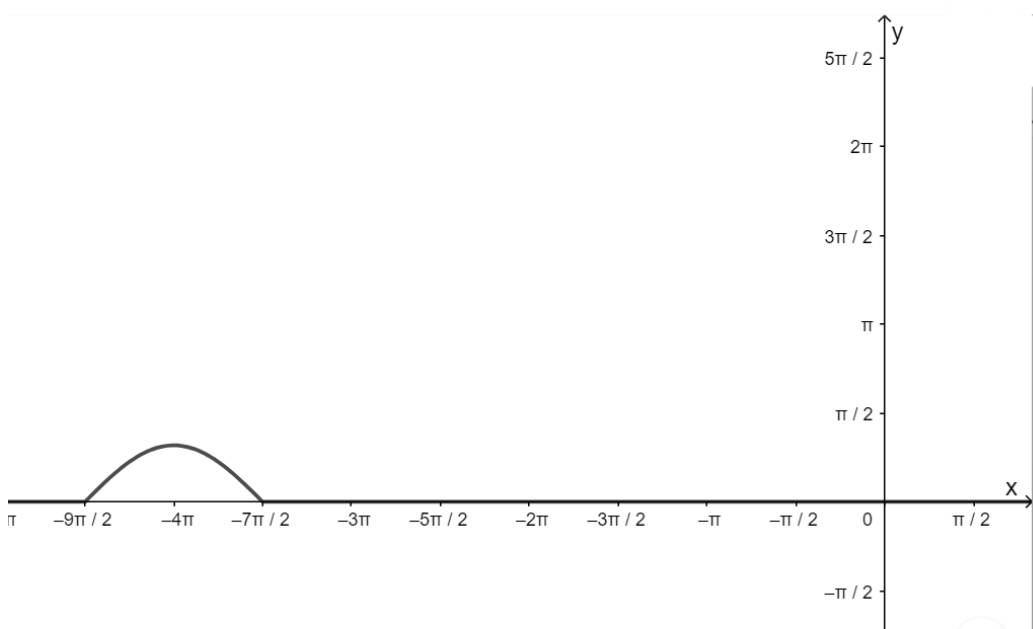
+ Đồng biến trên khoảng \(\left( { - \frac{{9\pi }}{2}; - 4\pi } \right)\)
+ Nghịch biến trên khoảng; \(\left( { - 4\pi ; - \frac{{7\pi }}{2}} \right)\)
- Khoảng \(\left( {\frac{{21\pi }}{2};\frac{{23\pi }}{2}} \right)\)
+ Vẽ đồ thị hàm số:
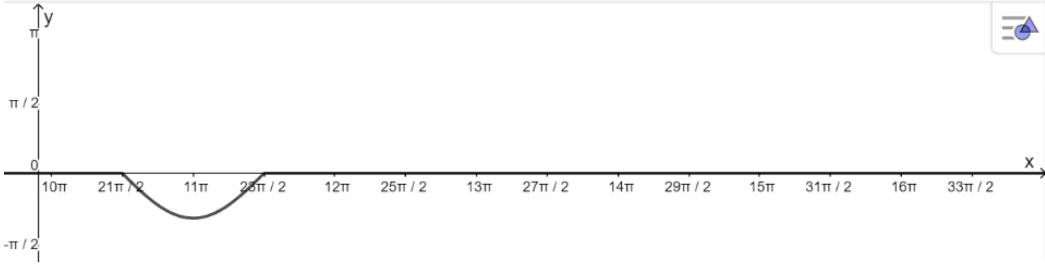
+ Đồng biến trên khoảng: \(\left( {11\pi ;\frac{{23\pi }}{2}} \right)\)
+ Nghịch biến trên khoảng: \(\left( {\frac{{21\pi }}{2};11\pi } \right)\)