Cho tứ diện ABCD. Gọi M,N lần lượt là trọng tâm ΔABD , ΔACD. Tìm :
a/ (AMN) ∩ (BCD)
b/ (DMN) ∩ (ACB)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn đáp án C
Ta có: MN là đường trung bình tam giác ACD.
=> CD // MN CD // (MNG)
Mặt khác: ![]()
Khi đó: Giao tuyến = ![]() = Gx // CD
= Gx // CD

Đáp án B
Vé hình ta thấy khối tứ diện MNPQ đồng dạng với tứ diệnABCD theo tỷ số k = 1 3
Do đó V M N P Q V A B C D = 1 3 3 = 1 27

Ta có:
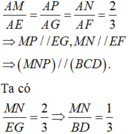
Ta có ∆ M N P đồng dạng với ∆ B C D theo tỉ số
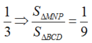
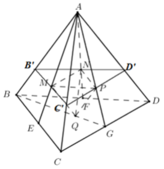
Dựng B ' C ' qua M và song song BC. C ' D ' qua P và song song với CD.
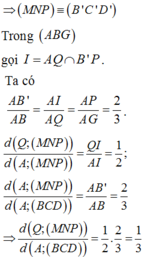

Chọn D.

Gọi I là trung điểm CD thì G 1 ∈ B I , G 2 ∈ A I ⇒ mặt phẳng ( B G 1 G 2 ) chính là mặt phẳng (ABI) ⇒ Thiết diện là tam giác cân AIB.
Đáp án C

Chọn D
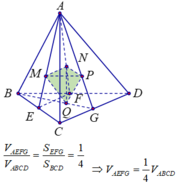
(Do E, F, G lần lượt là trung điểm của BC, BD, CD).
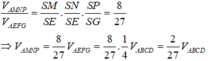
Do mặt phẳng (MNP) (BCD) nên
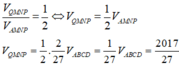

Hướng dẫn (khuya quá rồi).
Trong mp (ADN), lấy Q thuộc AD sao cho \(NP||GQ\)
\(\Rightarrow\left(\overrightarrow{MG};\overrightarrow{NP}\right)=\left(\overrightarrow{MG};\overrightarrow{GQ}\right)=180^0-\widehat{MGQ}\)
Áp dụng định lý hàm cos là tính được (\(GP=\dfrac{2}{3}NP\) ; tính MQ dựa vào hàm cos tam giác AMQ)

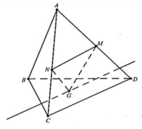

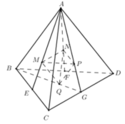
Nối AM cắt BD tại E \(\Rightarrow\) E là trung điểm BD
Nối AN cắt CD tại F \(\Rightarrow\) F là trung điểm CD
\(EF=\left(AMN\right)\cap\left(BCD\right)\)
Tương tự câu a, gọi P và Q lần lượt là trung điểm AB và AC thì \(PQ=\left(DMN\right)\cap\left(ACB\right)\)