a) tìm các cặp số nguyên (x, y)| Thỏa mãn 6x+5y+18=2xy
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
TM
Trần Mạnh
24 tháng 9 2020
Đúng(0)
Những câu hỏi liên quan
VN
1
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 8 2021
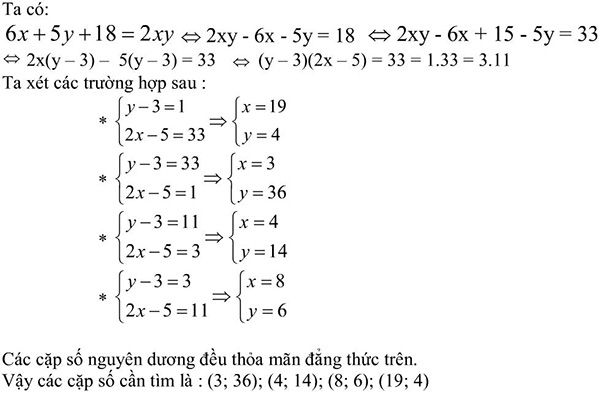
\(\Leftrightarrow2xy-6x-5y=18\)
\(\Leftrightarrow2x\left(y-3\right)-5\left(y-3\right)=33\)
\(\Leftrightarrow\left(2x-5\right)\left(y-3\right)=33\)
Phương trình ước số cơ bản
MP
1
25 tháng 9 2019
Ta có: \(6x+5y+18=2xy\)
\(\Leftrightarrow6x+5y-2xy=-18\)
\(\Leftrightarrow2x\left(3-y\right)+5y=-18\)
\(\Leftrightarrow2x\left(3-y\right)+5y-15=-18-15\)
\(\Leftrightarrow2x\left(3-y\right)+5\left(y-3\right)=-33\)
\(\Leftrightarrow2x\left(3-y\right)-5\left(3-y\right)=-33\)
\(\Leftrightarrow\left(3-y\right)\left(2x-5\right)=-33\)
Dễ rồi
VN
1
30 tháng 9 2021
\(6x+5y+18=2xy\\ \Leftrightarrow2xy-6x+15-5y=33\\ \Leftrightarrow2x\left(y-3\right)-5\left(y-3\right)=33\\ \Leftrightarrow\left(2x-5\right)\left(y-3\right)=33\)
Ta có:
| \(2x-5\) | ±33 | ±1 | ±3 | ±11 |
| \(y-3\) | ±1 | ±33 | ±11 | ±3 |
| \(x\) | 19;-14 | 3;2 | 4;1 | 8;-3 |
| \(y\) | 4;2 | 36;-30 | 14;-8 | 6;0 |
Vậy \(\left(x;y\right)=\left\{\left(19;4\right);\left(-14;2\right);\left(3;36\right);\left(2;-30\right);\left(4;14\right);\left(1;-8\right);\left(8;6\right);\left(-3;0\right)\right\}\)
TP
1
5 tháng 11 2017
ta có: \(6x+5y+15=2xy.\)
\(\Leftrightarrow2x\left(3-y\right)-5\left(3-y\right)=-30\)
\(\Leftrightarrow\left(2x-5\right)\left(3-y\right)=-30\)
mà 2x-5 là số lẻ nên \(2x-5\in\left\{1;-1;3;-3;5;-5;15;-15\right\}\)
\(\Leftrightarrow x\in\left\{3;2;4;1;5;0;10;-5\right\}\)
\(\Leftrightarrow y\in\left\{33;-27;13;-7;9;-3;5;1\right\}\)
NQ
2
1L
2
26 tháng 1 2023
pt này không phân tích thành nhân tử để làm được đáng lẽ ra 4y thì sẽ làm được ấy bạn
26 tháng 1 2023
=>4xy+6x-10y=20
=>2y(2x-5)+6x-15=5
=>(2x-5)(2y+3)=5
=>\(\left(2x-5;2y+3\right)\in\left\{\left(1;5\right);\left(5;1\right);\left(-1;-5\right);\left(-5;-1\right)\right\}\)
=>\(\left(x,y\right)\in\left\{\left(3;1\right);\left(5;-1\right);\left(2;-4\right);\left(0;-2\right)\right\}\)
TL
0