Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: góc BHD+góc BMD=180 độ
=>BHDM nội tiếp
b: BHDM nội tiếp
=>góc HDM+góc HBM=180 độ
=>góc ADM=góc ABC
=>góc ADM=góc ADC
=>DA là phân giáccủa góc MDC
c: Xét tứ giác DHNC có
góc DHC=góc DNC=90 độ
=>DHNC nội tiếp
=>góc NHD=góc NDC
góc NHD+góc MHD
=180 độ-góc NCD+góc MBD
=180 độ+180 độ-góc ABD-góc ACD
=180 độ
=>M,H,N thẳng hàng
a) Xét tứ giác KEDC có
\(\widehat{KEC}\) và \(\widehat{KDC}\) là hai góc đối
\(\widehat{KEC}+\widehat{KDC}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: KEDC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
Tâm của đường tròn này là trung điểm của KC
a: CD//AB
=>\(\widehat{CDB}=\widehat{ABC}\)
Xét (O) có
\(\widehat{DBC}\) là góc tạo bởi dây cung BC và tiếp tuyến BD
\(\widehat{BAC}\) là góc nội tiếp chắn cung BC
Do đó: \(\widehat{DBC}=\widehat{BAC}\)
Xét ΔDBC và ΔCAB có
\(\widehat{DBC}=\widehat{CAB}\)
\(\widehat{DCB}=\widehat{ABC}\)
Do đó: ΔDBC đồng dạng với ΔCAB
=>\(\dfrac{DC}{CB}=\dfrac{BC}{AB}\)
=>\(BC^2=AB\cdot DC\)
a: góc OAD+góc OMD=180 độ
=>OADM nội tiếp
b: ΔOBC cân tại O
mà ON là đường cao
nên ONlà trung trực của BC
=>sđ cung NB=sd cung NC
=>góc BAN=góc CAN
=>AN là phân giác của góc BAC
góc DAI=1/2*sđ cung AN
góc DIA=1/2(sđ cung AB+sđ cung NC)
=1/2(sđ cung AB+sđ cung NB)
=1/2*sđ cung AN
=>góc DAI=góc DIA
=>ΔDAI cân tại D
a) Ta có: \(\angle AEH+\angle AFH=90+90=180\Rightarrow AEHF\) nội tiếp
b) AEHF nội tiếp \(\Rightarrow\angle EFA=\angle EHA=90-\angle BHE=\angle ABC\)
c) Ta có: \(\angle OAC=\dfrac{180-\angle AOC}{2}=90-\dfrac{1}{2}\angle AOC=90-\angle ABC\)
\(\Rightarrow\angle OAC+\angle ABC=90\Rightarrow\angle OAC+\angle AFE=90\Rightarrow OA\bot EF\)
a: Xét tứ giác BCEF có \(\widehat{BFC}=\widehat{BEC}=90^0\)
nên BCEF là tứ giác nội tiếp đường tròn đường kính BC
Kẻ tiếp tuyến Ax của (O)
=>Ax\(\perp\)OA tại A
Xét (O) có
\(\widehat{xAC}\) là góc tạo bởi tiếp tuyến Ax và dây cung AC
\(\widehat{ABC}\) là góc nội tiếp chắn cung AC
Do đó: \(\widehat{xAC}=\widehat{ABC}\)
mà \(\widehat{ABC}=\widehat{AEF}\left(=180^0-\widehat{FEC}\right)\)
nên \(\widehat{xAC}=\widehat{AEF}\)
mà hai góc này là hai góc ở vị trí so le trong
nên Ax//FE
ta có: Ax//FE
OA\(\perp\)Ax
Do đó: OA\(\perp\)FE
b: Xét (O) có
ΔACK nội tiếp
AK là đường kính
Do đó: ΔACK vuông tại C
Xét (O) có
\(\widehat{ABC}\) là góc nội tiếp chắn cung AC
\(\widehat{AKC}\) là góc nội tiếp chắn cung AC
Do đó: \(\widehat{ABC}=\widehat{AKC}\)
Xét ΔADB vuông tại D và ΔACK vuông tại C có
\(\widehat{ABD}=\widehat{AKC}\)
Do đó: ΔADB~ΔACK
=>\(\dfrac{AD}{AC}=\dfrac{AB}{AK}\)
=>\(AD\cdot AK=AB\cdot AC\)
a) Xét tứ giác AEDB có
\(\widehat{AEB}=\widehat{ADB}\left(=90^0\right)\)
nên AEDB là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
AB, M
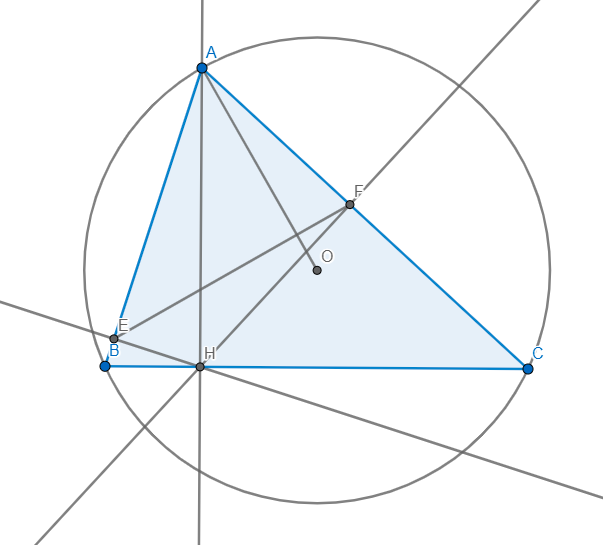
Ta có ; \(\widehat{A_1}=\widehat{A_2}\left(gt\right)\)
=> D là điểm chính giữa cung BC
=> DO vuông góc với BC tại trung điểm H của BC
lại có: \(\Delta BDM~\Delta BCF\Rightarrow\frac{BD}{BC}=\frac{DM}{CF}\Rightarrow\frac{BD}{2BH}=\frac{\frac{1}{2}DA}{CF}\Rightarrow\frac{BD}{BH}=\frac{DA}{CF}\)
Mà \(\widehat{D_1}=\widehat{C_2}\)( bẹn chứng minh ở phần a nhé)
\(\Rightarrow\Delta BDA~\Delta HCF\left(c.g.c\right)\Rightarrow\widehat{F_1}=\widehat{A_1}\)(2 góc tương ứng)
Mà A1=A2(gt) và A2=E1(cùng chắn 1 cung DC).
F1=E1=> tam giác EFHC nội tiếp