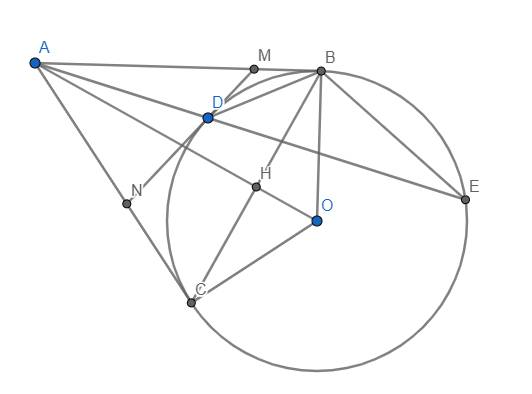
Từ một điểm A nằm ngoài đường tròn tâm O, bán kính R (AO<2R) vẽ 2 tiếp tuyến AD, AE với (O) (D, E là các tiếp điểm). Gọi H là giao điểm của DE và AO. M là điểm thuộc cungnhỏ DE (M khác D, khác E, MD < ME). Tia AM cắt đường tròn (0; R) tại N. Đoạn thẳng AO cắt cung nhỏ DE tại K. a) Chứng minh AO vuông góc với DE và AD^2=AM.AN. b) C/m NK là tia phân giác của góc DNE và tứ giác MHON noi tiếp. c) Kè đưong kính KQ của đường tròn (O; R). Tia QN cắt tia ED tại C. Chứng minh MD.CE = ME.CD.
ai giúp mình với đi ạ please thanks thanks