Giúp mình với, giải thích thật kĩ cho mình hiểu nha
Tìm số nguyên x
A=8x+5/2x+3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
17 tháng 6 2016
1. Định nghĩa:
Số hữu tỉ là số viết dưới dạng phân số \(\frac{a}{b}\) với a; b \(\in\)Z(tập hợp số nguyên) b\(\ne\)0
2. Kí hiệu:
Tập hợp các số hữu tỉ kí hiệu là Q
LN
3
25 tháng 10 2015
các kí hiệu toán học thường bắt đầu từ chữ đầu tiên trong tiếng anh. số nguyên tố trong tiếng anh là prime number nên cô giáo viết là P.
mình nghĩ vậy
22 tháng 3 2020
a,
Vì -4 chia hết cho x-5
=> x-5 thuộc Ư(-4)
Ta có: Ư(-4) = {+_1 ; +_2 ; +_4}
=> x-5 thuộc {+_1 ; +_2 ; +_4}
=> x thuộc {6;4;7;3;9;1}
Vậy ....
b,
x-3 chia hết cho x+1
=> x+1-4 chia hết cho x+1
Mà x+1 chia hết cho x+1
=> 4 chia hết cho x+1
=> x+1 thuộc Ư(4)
Ta có: Ư(4) = {+_1 ; +_2 ; +_4}
=> x+1 thuộc {+_1 ; +_2 ; +_4}
=> x thuộc {0;-2;1;-3;3;-5}
Vậy ....
c,
2x-6 chia hết cho 2x+2
=> 2x+2-8 chia hết cho 2x+2
Mà 2x+2 chia hết cho 2x+2
=> 8 chia hết cho 2x+2
=> 2x+2 thuộc Ư(8)
Ta có: Ư(8) = {+_1 ; +_2 ; +_4 ; +_8}
=> 2x+2 thuộc {+_1 ; +_2 ; +_4 ; +_8}
=> 2x thuộc {-1;-3;0;-4,2;-6;6;-10}
=> x thuộc {-0.5;-1.5;0;-2;1;-3;3;-5}
Vậy ...
TC
26 tháng 5 2022
\(M=\dfrac{10n+25}{2n+4}=\dfrac{5\left(2n+5\right)}{2n+4}=5\cdot\dfrac{2n+4}{2n+4}+\dfrac{1}{2n+4}\)
để M ∈ Z
=> \(2n+4\inƯ\left\{1\right\}=\left\{-1;1\right\}\)
\(=>\left\{{}\begin{matrix}2n+4=1\\2n+4=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2n=-3\\2n=-5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}n=-\dfrac{3}{2}\\n=-\dfrac{5}{2}\end{matrix}\right.\) thì M ∈Z
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 7 2021
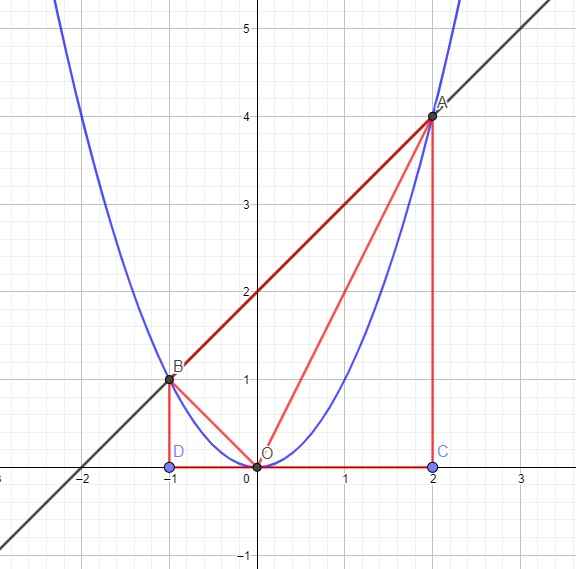
1.
Dễ dàng tìm được tọa độ 2 giao điểm, do vai trò của A, B như nhau, giả sử \(A\left(2;4\right)\) và \(B\left(-1;1\right)\)
Gọi C và D lần lượt là 2 điểm trên trục Ox có cùng hoành độ với A và B, hay \(C\left(2;0\right)\) và \(D\left(-1;0\right)\)
Khi đó ta có ABDC là hình thang vuông tại D và C, các tam giác OBD vuông tại D và tam giác OAC vuông tại C
Độ dài các cạnh: \(BD=\left|y_B\right|=1\) ; \(AC=\left|y_A\right|=4\)
\(OD=\left|x_D\right|=1\) ; \(OC=\left|x_C\right|=2\) ; \(CD=\left|x_C-x_D\right|=3\)
Ta có:
\(S_{OAB}=S_{ABDC}-\left(S_{OBD}+S_{OAC}\right)\)
\(=\dfrac{1}{2}CD.\left(AC+BD\right)-\left(\dfrac{1}{2}BD.OD+\dfrac{1}{2}AC.OC\right)\)
\(=\dfrac{1}{2}.3.\left(4+1\right)-\left(\dfrac{1}{2}.1.1+\dfrac{1}{2}.4.2\right)=3\)
H
29 tháng 5 2023
Bài này làm khá tắt chỗ 3 điểm cực trị, mình trình bày lại để bạn dễ hiểu nhé!
.......
Để y' = 0\(\Leftrightarrow\left[{}\begin{matrix}x=1\\f'\left(\left(x-1\right)^2+m\right)=0\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=1\\\left(x-1\right)^2+m=-1\\\left(x-1\right)^2+m=3\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=1\\\left(x-1\right)^2=-1-m\left(1\right)\\\left(x-1\right)^2=3-m\left(2\right)\end{matrix}\right.\)
Để hàm số có 3 điểm cực trị thì y' = 0 có 3 nghiệm phân biệt.
Ta có 2 trường hợp.
+) \(TH_1:\) (1) có nghiệm kép x = 1 hoặc vô nghiệm và (2) có hai nghiệm phân biệt khác 1.
\(\Rightarrow\left[{}\begin{matrix}-1-m\le0\\3-m>0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}m\ge-1\\m< 3\end{matrix}\right.\) \(\Leftrightarrow-1\le m< 3\)
+) \(TH_2:\) (2) có nghiệm kép x = 1 và (2) có một nghiệm phân biệt khác 1.
\(\Rightarrow\left[{}\begin{matrix}-1-m>0\\3-m\le0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}m< -1\\m\ge3\end{matrix}\right.\) \(\Leftrightarrow m\in\varnothing\)
\(\Rightarrow-1\le m< 3\Rightarrow S=\left\{-1;0;1;2\right\}\)
Do đó tổng các phần tử của S là \(-1+0+1+2=2\)
Để A=\(\frac{8x+5}{2x+3}\)là số nguyên \(\Leftrightarrow\)\(8x+5⋮2x+3\)
Ta có: \(8x+5=(8x+12)+5-12=\left(8x+12\right)-7⋮2x+3\)
vì \(8x+12⋮2x+3\)nên \(7⋮2x+3\)\(\Rightarrow2x+3\inƯ\left(7\right)\Rightarrow2x+3\in\xi-7;-1;1;7\xi\Rightarrow2x\in\xi-10;-4;-2;4\xi\)\(\Rightarrow x\in\xi-5;-2;-1;2\xi\)