Tam giác ABC đường cao BD và CE cắt nhau tại H a/ Chứng minh ED/AH = sinA
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
JM
0
3 tháng 7 2018
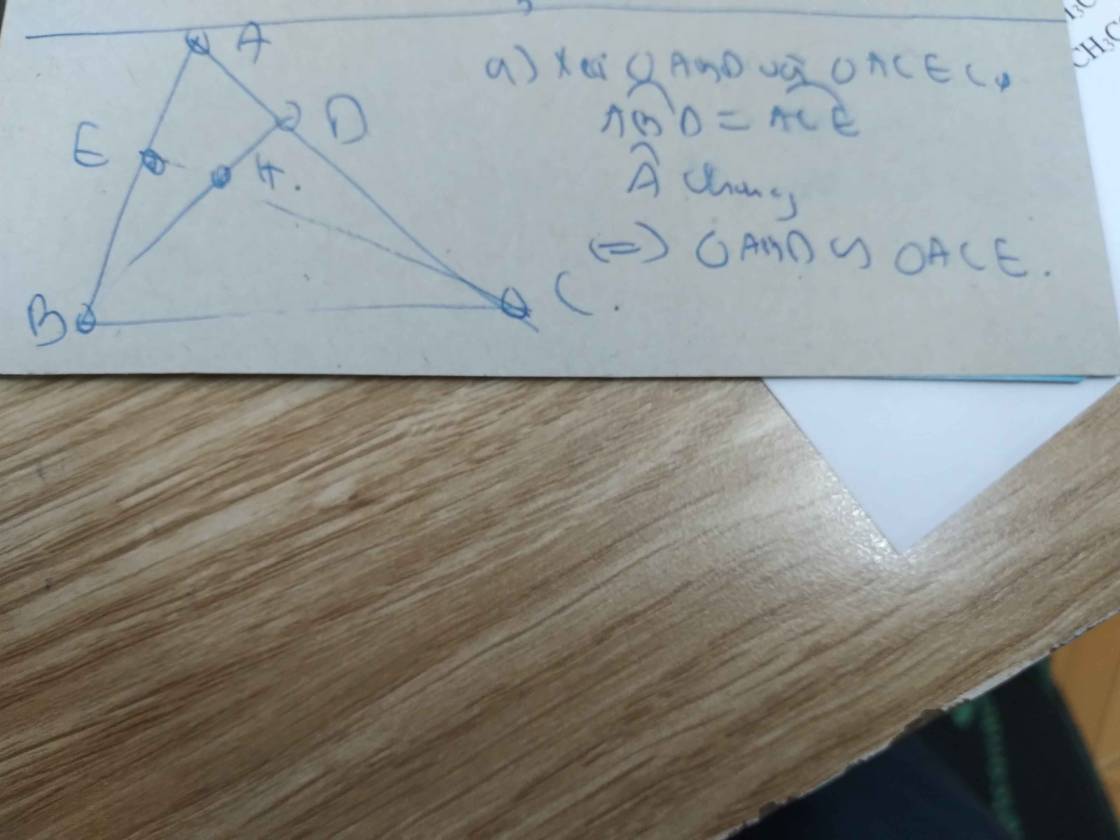
a, Xét ∆ ABD và ∆ ACE có:
Góc D = góc E = 90°
AB = AC (∆ ABC cân)
Góc BAC chung
➡️∆ ABD = ∆ ACE (ch-gn)
➡️AD = AE (2 cạnh t/ư)
b, ✳️C/m AH là tia phân giác của góc BAC
Xét∆ ABC cân tại A có:
BD vuông góc với AC
CE vuông góc với AB
H là giao điểm của BD và CE
➡️H là trực tâm ∆ ABC
➡️AH vuông góc với BC
mà ∆ ABC cân tại A
➡️AH là đg cao đồng thời là đg phân giác
➡️AH là p/g góc BAC(đpcm)
✳️C/m AH là đg trung trực của ED
Xét ∆ AED cân tại A (AD = AE)
➡️AH là đg phân giác đồng thời là đg trung trực
➡️AH là đg trung trực của ED (đpcm)
c, Xét ∆ AEH và ∆ ADH có:
AE = AD (cmt)
Góc BAH = góc CAH (cmt)
AH chung
➡️∆ AEH = ∆ ADH (c.g.c)
➡️HE = HD (2 cạnh t/ư)
Xét ∆ CDH vuông tại D
➡️CH > HD
mà HE = HD (cmt)
➡️CH > HE
Còn câu d để mk nghĩ đã nhé
4 tháng 7 2018
Câu d nè bn.
d, Vì AH là đg trung trực của EF và AH vuông góc với BC
➡️ED // BC (quan hệ từ vuông góc đến song song)
Ta có: góc FED = góc DBC (2 góc có 2 cạnh tương ứng song song)
Gọi AH giao BC tại M
Xét ∆ ABC cân tại A
➡️AH là đg cao đồng thời là trung tuyến
HM là trung tuyến của BC
Xét ∆ IBC có HM là đg cao đồng thời là trung tuyến
➡️∆ IBC cân tại I
➡️Góc DBC = góc ECB
Mà góc ECB = góc DEC (2 góc so le trong)
➡️Góc DEC = góc DBC
mà góc DBC = góc FED (cmt)
➡️Góc FED = góc DEC
➡️ED là tia phân giác góc FEC
Xét ∆ FEC có: CI là phân giác góc DCE (gt)
EI là phân giác góc FEC (cmt)
CI và EI giao nhau tại I
➡️I là tâm đg tròn nội tiếp∆ FEC
➡️FI là phân giác góc CFE
mà góc CFE vuông (EF // BD, góc BDC = 90°)
➡️Góc EFI = góc CFI = 90° ÷ 2 = 45°
Vậy góc EFI = 45°
Hok tốt nhé~
CM
25 tháng 2 2019
Chú ý H là trực tâm tam giác ABC, từ đó AH vừa là đường cao vừa là đường phân giác
28 tháng 4 2021
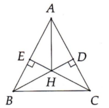
a) Xét ΔABD vuông tại D và ΔACE vuông tại E có
AB=AC(ΔABC cân tại A)
\(\widehat{BAD}\) chung
Do đó: ΔABD=ΔACE(cạnh huyền-góc nhọn)
Suy ra: BD=CE(hai cạnh tương ứng)
28 tháng 4 2021
b) Ta có: ΔABD=ΔACE(cmt)
nên AD=AE(Hai cạnh tương ứng)
Xét ΔADE có AD=AE(cmt)
nên ΔADE cân tại A(Định nghĩa tam giác cân)
Giải thích các bước giải:
Ta có:
\(\Delta ADB\)và \(\Delta\widehat{ADB}=90^o\)
\(\Rightarrow sinA=\frac{BD}{AB}\left(1\right)\)
\(\hept{\begin{cases}\widehat{BEH}=\widehat{BDA}=90^o\\\widehat{B}chung\end{cases}}\)
\(\Rightarrow\Delta BEH~\Delta BDA\left(g.g\right)\)
\(\Rightarrow\frac{BE}{BD}=\frac{BH}{BA}\)
\(\Rightarrow\frac{BE}{BH}=\frac{BD}{BA}\)
Khi đó:
\(\hept{\begin{cases}\widehat{B}chung\\\frac{BE}{BH}=\frac{BD}{BA}\end{cases}}\)
\(\Rightarrow\Delta BED~\Delta BHA\left(g.g\right)\)
\(\Rightarrow\frac{ED}{HA}=\frac{BD}{BA}\left(2\right)\)
\(\left(1\right),\left(2\right)\Rightarrow\frac{ED}{HA}=sinA\)